Precisamos de mais slogans (sobre as reclamações do CAEPRO)

Este é o segundo dos dois vídeos sobre didática que eu fiz
em março/2023 inspirado pelas reclamações do CAEPRO.
O primeiro vídeo é este aqui: "Visual vs. auditivo".
Pra assistir este vídeo clique ou no thumbnail abaixo
ou nas marcas de tempo nas legendas.
As legendas dele em Lua estão aqui.
Versão em PDF desta página.

Alguns dos trechos que eu acho mais importantes:
01:10 até 08:51: duas histórias verídicas sobre GA (e chutar e testar)
08:54 até 18:23: alguns exercícios vão mudando com o tempo
18:28 até 24:12: vários modos de estudar pelo livro
28:14 até 29:42: se transformar numa pessoa autônoma
29:44 até 32:22: eu não posso fazer o papel do colega muito seu amigo
32:26 até 33:12: ...que vale a pena estudar com você
33:35 até 36:36: indicar graus de certeza
54:07 até 57:47: Henrique e Google Drive
1:11:02 até 1:17:42: seja o seu prório Geogebra
1:22:24 até 1:24:18: coisas que valem a pena compartilhar e são menos óbvias
1:29:07 até 1:39:03: todas as perguntas eram bem vindas
1:39:46 até 1:45:02: experimentar vários papéis / o que funciona a longo prazo

Links pra algumas coisas que eu menciono no vídeo:
   Sapt#legendas: Sobre aulas por Telegram
   Mpg: Material complementar para Geometria Analítica
   2aT6: Aprender a testar vai ser a coisa mais importante do curso
   2dT4: Releia a Dica 7
   3bT83: Cortes numa superfície: gabarito
   3cL2m6: R^3 em papel
   3cT75: Pirâmide e cruz
   2gT17: Alex, Bob, Carlos e as retas reversas
   2fT114: Questão sobre o TFC2: gabarito (2022.2)
   Árvores em Maxima e SymPy
   2gT7: A linguagem de Cálculo 2: péssimas notícias
   CalcEasy: Vídeo do Mathologer sobre o "Calculus Made Easy"
   Cabos: Cabos na diagonal
   2fT63: Retângulos com lados negativos
   Sapt39:27: Sobre aulas por Telegram: fala do Henrique Sá Earp
   3dT64: Calculus Made Easy: o exemplo da escada
   GeoGebra: All about Sliders!
   4gT5: Seja o seu próprio GeoGebra
   3dT26: Vídeo sobre splines da Freya Holmér
   2eT95: Integral como limite
   2fT66: Jeito esperto e exercício das montanhas
   Maxima Workbook: Simplification
   2cL2e79: vira a melhor pessoa do mundo pra mim
   Somas: Dicas de estudo pro "integrais como somas de retângulos"
   2gT11: me dá um exemplo e vamos discutir o exemplo
   2fT135: EDOs com os truques do anexo
   2dT5: Contexto

00:00 Oi gente, esse é o meu segundo vídeo
00:03 sobre didática motivado pelas reclamações
00:06 do CAEPRO. O título curto desse vídeo vai
00:09 ser "Precisamos de mais slogans" - eu vou
00:11 explicar isso daqui a pouco, e eu vou
00:14 fazer esse vídeo naquele esquema de
00:15 vídeos para pessoas que odeiam vídeos,
00:18 no seguinte sentido: de todas as pessoas
00:21 que eu conheço só tem uma pessoa que
00:23 prefere assistir o vídeo de verdade com
00:26 legendas a simplesmente ler as legendas
00:29 sem o vídeo...
00:31 ler as legendas super rápido
00:33 e assistir o vídeo só nos pedacinhos
00:35 em que ela quer ver a imagem.

00:38 Então basicamente eu vou gravar esse
00:40 vídeo, eu vou legendar esse vídeo da
00:43 mesma forma que eu tou fazendo com os
00:45 outros, em que eu crio páginas como isso
00:47 aqui, em que as legendas estão aqui, e se
00:50 a pessoa quiser assistir o trecho do
00:51 vídeo ela clica, sei lá, aqui, e aí esse
00:53 link vai pro YouTube, e a pessoa
00:55 assiste aquele pedacinho.

00:57 Então...
01:00 deixa eu começar esse vídeo. O melhor
01:03 jeito de começar esse vídeo não é por um
01:06 resumo, é por uma história, tá... aliás, por
01:08 uma série de histórias.

01:10 Eu vou começar contando algumas histórias
01:12 sobre Geometria Analítica...
01:17 primeiro várias histórias verídicas.
01:20 Quando eu comecei a dar aula no Pólo
01:23 Universitário de Rio das Ostras - o PURO -
01:25 uma das matérias que eu comecei a dar...
01:27 que eu tava dando nessa época era
01:30 Geometria Analítica, que é uma matéria
01:31 pesadíssima de primeiro período...
01:34 e eu tentava dar essa aula como eu tinha
01:37 aprendido... eu tinha feito graduação,
01:39 mestrado e doutorado em Matemática, e
01:41 quando a gente estuda Matemática
01:44 todas as nossas aulas são dadas no
01:47 esquema de "proposição, teorema,
01:48 demonstração"...

01:49 e eu tentava dar minhas aulas de
01:52 Geometria Analítica desse jeito e não
01:54 funcionava... e tinha várias outras coisas
01:57 que eu tentava dar naquela época e
01:58 também não funcionavam... por exemplo, eu
02:00 tentava dar
02:02 exercícios, deveres de casa e questões de
02:05 prova que tivessem itens com "escreva com as
02:08 suas palavras", e os resultados eram
02:10 catastróficos... eu não vou dar os detalhes
02:12 aqui porque os detalhes tão muito bem
02:15 explicados naquele vídeo
02:18 cujo título é "Sobre aulas por
02:19 Telegram"...

02:21 Então, nesse trecho aqui que começa no
02:24 2:15, eu consegui explicar muito bem
02:26 o que que aconteceu nessa época, e de um
02:28 jeito muito conciso,
02:30 porque eu ensaiei muito e aí eu consegui uma
02:33 explicação maravilhosa naquela época.

02:36 Agora deixa eu contar uma história que
02:39 aconteceu com uma aluna.
02:41 A aluna veio me perguntar como é que a gente
02:43 calculava a interseção de duas retas...
02:47 e aí eu comecei a explicar para ela
02:49 mostrando a coisa bem passo a passo,
02:51 mostrando que que cada letra...
02:53 qual é a
02:56 interpretação geométrica do que cada
02:59 letra queria dizer,
03:01 transformando idéias geométricas em
03:03 idéias algébricas, e não sei que, e a aluna foi
03:06 ficando DESESPERADA, e numa hora ela disse:
03:08 "PROFESSOR, QUAL É A FÓRMULA?"... então, repara,
03:13 essa aluna... ela queria decorar um método.

03:16 A gente acha que os alunos não vão
03:19 chegar na faculdade nesse esquema de
03:21 querer "decorar o método", mas eles chegam
03:23 aos milhares, quase todo mundo chega na
03:26 faculdade ainda achando que nas matérias
03:28 de Matemática eles vão ter que
03:29 decorar métodos...

03:31 Agora deixa eu contar uma outra história,
03:33 que é ainda pior, tá... é o seguinte.
03:36 eu tentava motivar os
03:41 assuntos de Geometria Analítica com idéias
03:45 geométricas e construções geométricas
03:46 que eram fáceis de entender, e que aos
03:48 pouquinhos a gente ia traduzir elas pra
03:51 versão algébrica delas...

03:54 E aí tinha um garoto, que eu vou me
03:56 referir ele como o Gênio da Turma, que
03:59 toda vez que eu começava a apresentar um
04:01 problema desses ele "adivinhava", entre
04:04 aspas, o resto... ele dizia EU SEI! EU SEI! EU
04:06 SEI RESOLVER! E aí ele aplicava um método
04:08 lá completamente bizarro, completamente
04:10 absurdo, chegava num resultado
04:12 completamente absurdo também...

04:15 E, repara:
04:16 1) ele achava que se ele "sabia"
04:20 o método esse método
04:23 automaticamente tava certo...
04:25 2) ele não achava importante testar a
04:27 resposta -
04:28 3) talvez ele nem soubesse a testar as
04:32 respostas... e 4) uma das piores coisas que
04:35 acontecia era o seguinte: os outros alunos
04:37 da turma ficavam impressionadíssimos
04:39 e achavam ele um gênio...
04:42 depois eu vou conectar sua história com
04:45 várias coisas, tá... em especial eu vou
04:47 conectar ela com a Dica 7, que eu já
04:50 mostrei um pouquinho no outro vídeo...
04:52 Mas vou voltar a ela depois - várias vezes.

04:57 Então, eu disse que eu ia falar sobre
04:59 slogans,
05:02 e que eu ia explicar aos pouquinhos em
05:04 que sentido eu tava usando a palavra
05:06 "slogan". O primeiro slogan que eu quero
05:09 mencionar aqui é "chutar e testar". Lembra
05:12 que esses alunos eles queriam decorar um
05:14 método, ou queriam aplicar um método, e
05:17 eles nem achavam importante testar se o
05:19 método deles estava certo ou não...

05:21 à medida que eu fui vendo que o meu
05:23 jeito de
05:24 ensinar Geometria Analítica "pra
05:27 matemáticos" tava dando
05:29 completamente errado uma das coisas que
05:32 eu comecei a fazer foi dar muita ênfase no
05:34 "vamos testar os nossos resultados" -
05:37 vamos testar nossas idéias, resultados, etc...

05:40 A partir de um certo momento eu
05:44 comecei a preparar um bocado de material
05:45 pra Geometria Analítica, e ele virou
05:47 essa coisa daqui, ó, que tem essa capinha,
05:50 e
05:52 o título é "Material Complementar para
05:54 Geometria Analítica". Eu fui fazendo isso
05:57 aos poucos ao longo de anos, e depois
05:59 transformei num PDF mais ou menos bacana,
06:02 que eu botei na minha página...

06:04 e isso aqui é a versão de 2018 desse PDF,
06:10 e isso aqui é a minha primeira versão
06:12 daquilo que virou aquele slide do
06:16 "Releia a Dica 7" - esse aqui...
06:20 então o texto é o mesmo, mas a
06:24 formatação é diferente...
06:26 e repara que isso aqui já começa com
06:29 essa dica 1,
06:31 que é
06:34 "aprenda a testar tudo: contas,
06:37 possíveis soluções de equações,
06:38 representações gráficas de conjuntos, etc..."

06:41 Então isso é uma das primeiras páginas
06:43 da introdução desse material,
06:47 e isso é a primeira dica -
06:49 isso já dá uma certa
06:52 ênfase para essa dica, né, mas mesmo isso
06:54 não era suficiente, eu precisava de mais
06:56 ênfase ainda para isso...

07:00 Em 2020, quando as aulas começaram a ser
07:03 online e quando eu comecei a pdfizar
07:06 muito material,
07:09 uma das primeiras coisas do meu material
07:11 de Cálculo 2 era isso aqui: a mesma idéia,
07:14 só que em letras garrafais...

07:17 Eu já
07:19 apresentava o curso de Cálculo 2
07:21 dizendo pras pessoas que Cálculo 2
07:23 não é Cálculo 1, Cálculo 2 não é
07:25 parecido com nenhuma matéria que eles já
07:26 tenham visto, a metodologia é diferente...
07:32 decorar métodos não vai funcionar porque
07:35 Cálculo 2 tem tantos métodos que se
07:37 eles tentarem decorar os métodos direito
07:39 eles vão precisar de uma cabeça de um
07:41 tamanho de um apartamento para caber
07:42 tudo... então o jeito mais garantido de
07:46 aprender o suficiente da matéria e se dar
07:48 bem na prova é aprender a testar tudo.

07:50 Então, um dos slogans mais básicos era
07:54 que "aprender a testar vai ser A coisa
07:58 mais importante do curso", e uma expressão
08:00 que eu repetia o tempo inteiro era "chutar
08:03 e testar"... então a todo momento quando a
08:07 gente via um problema novo a gente
08:08 começava tentando resolver ele por
08:10 chutar e testar...

08:12 Ao invés da gente aprender direto o
08:14 método que vai resolver o problema direto e
08:17 rápido, a gente começava chutando
08:19 soluções e testando se cada solução tava
08:22 certa ou não... e em geral eu começava com
08:26 exemplos muito simples em que
08:30 depois de dois ou três chutes algumas
08:33 pessoas já conseguiam entender a mecânica
08:35 daquele problema e conseguiam chegar
08:37 direto no chute certo, em que os valores
08:39 eram muito simples...

08:42 E aí depois a gente passava para coisas
08:44 em que o chutar e testar não
08:46 funcionava mais,
08:48 mas a gente começava sempre pelo chutar
08:51 e testar.

08:54 Uma coisa que eu quero comentar aqui é o
08:57 seguinte.
08:58 Vários dos exercícios, slogans e
09:01 historinhas que eu usava iam mudando com o
09:03 tempo. Deixa eu começar com exemplos.

09:05 Primeiro, Cálculo 3 é uma matéria em que
09:10 a gente basicamente aprende a visualizar
09:12 coisas tanto em 2D quanto em 3D...

09:15 Antes da pandemia eu passava uma ou duas
09:19 aulas em que a gente fazia umas
09:20 atividades de construir umas figuras em
09:22 3D dadas para equações, mas a gente
09:25 construía elas com arame e papel, e os
09:27 alunos trabalhavam em grupo, e aí eles
09:30 iam apontando para essas figuras com
09:32 caneta e eles conseguiam descrever
09:34 curvas sobre a superfície das figuras,
09:36 conseguiam descrever pontos na
09:38 superfície das figuras, e como eles
09:40 estavam trabalhando em grupo
09:43 eles tinham que treinar apontar pra
09:45 essas coisas de um jeito que os colegas
09:48 entendessem...
09:50 e isso acabava sendo muito útil.

09:54 Eu falei um pouquinho sobre isso na minha
09:58 apresentação sobre aulas por Telegram, o
10:00 slide sobre isso é esse aqui, mas eu não
10:03 vou ler ele agora, vou deixar
10:06 o link nas legendadas disso aqui... e se
10:10 alguém quiser ver o trecho do
10:12 vídeo em que eu falo sobre isso o trecho
10:14 é esse, a legendas são essas aqui, ó...
10:17 deixa eu aumentar um pouquinho

10:20 quando a gente fazia aulas presenciais a
10:23 gente passava vários dias de aula
10:24 montando figuras em R^3 com arame e papel
10:26 em grupo, etc, etc...

10:34 E, bom, aí começou a pandemia...
10:37 e aí eu tive que adaptar esse método um
10:40 pouquinho pras pessoas poderem fazer
10:41 algo parecido em casa... aí eu dei essas
10:45 dicas aqui pra elas... eu continuava
10:47 tentando fazer exercício parecidos, e eu
10:50 disse para elas: vamos fazer um modelo de
10:52 R^3 - aqui na verdade é um modelo só da
10:55 parte de R^3 em que todas as coordenadas são
10:58 maiores ou iguais a 0 - então eu ensinava as
11:00 pessoas a dobrarem o papel desse jeito
11:02 daqui... isso aqui é tipo um quadrante
11:04 de R^3... putz, era pra eu ter pesquisado
11:07 qual o nome de
11:10 "quadrante em R^3", mas eu esqueci...

11:15 E aí as pessoas iam usar uma caneta para
11:17 apontar pontos aqui, e aí com isso elas
11:20 vão conseguir visualizar determinadas
11:22 retas muito simples, depois determinados
11:24 planos muito simples, e coisas assim... e eu
11:27 também dava uma dica na página seguinte ó,
11:30 que é que depois que você fizer essa
11:34 essa coisa em papel você pode fazer um
11:37 quadriculado nela e tudo vai ficar bem
11:40 mais fácil.

11:42 e repara que até tem uma coisa implícita
11:44 aqui, que aqui se você conseguir fazer a
11:47 distância entre cada unidade e a outra
11:49 ficar parecida
11:51 fica tudo muito mais fácil... alguns alunos
11:54 não tinham prática com isso e a
11:56 distância entre o 0 e 1 deles era,
11:57 sei lá, o triplo da distância entre o 1 e
12:00 o 2, mas depois de um pouquinho de
12:02 prática eles viam que se eles caprichassem
12:04 um pouquinho mais em deixar as
12:05 distâncias parecidas tudo ficava muito
12:07 mais fácil de visualizar...

12:10 Então...
12:13 voltando, eu tava falando como é que meus
12:15 exercícios iam mudando com o tempo à
12:17 medida que eu ia adaptando eles pros
12:18 alunos...

12:20 e num dos primeiros semestres da
12:22 pandemia
12:25 eu passei umas figuras que um dos livros
12:29 que a gente tava usando usava...

12:32 eu passei uns exercícios disso, de
12:34 desenhar cortes nessa figura...
12:37 deixa eu mostrar aqui como é que eram
12:39 essas coisas...

12:41 então a gente fez alguns exercícios em
12:44 sala - quer dizer, durante as aulas por
12:46 Telegram - e depois teve um mini-teste
12:48 sobre isso, e os mini-testes duravam 24
12:51 horas...

12:53 e nesse mini-teste a questão era a
12:56 seguinte. Eu pegava essa figura daqui, do
12:59 livro do Thomas,
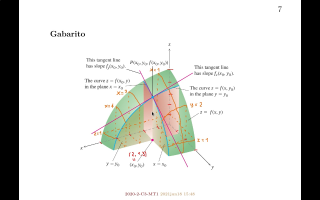
13:05 eu dizia que esse ponto (x0,y0) daqui era
13:09 o ponto (2,1.3),
13:12 e eu dava mais algumas dicas, e eu pedia
13:15 para os alunos calcularem...
13:17 ah olha só! "Leia a dica 7" aqui, ó!
13:19 Peraí...

13:21 Mas voltando. Eu pedia pros alunos
13:23 calcularem a interseção dessa
13:25 superfície daqui...
13:27 dessa superfície aqui, que tá desenhada
13:29 cortada... nesse trecho aqui a superfície
13:32 curva não tá desenhada, mas dá para
13:33 imaginar como ela é...

13:35 Eu pedia pra eles
13:39 representarem graficamente como ia ser
13:41 a interseção dessas superfícies daqui com
13:43 esses planos daqui... o plano com x=1,
13:46 o plano com x=3, o plano com x=4,
13:48 depois o plano com y=2, depois o plano
13:51 com z=1.

13:54 E aí aqui tem um gabarito, que
13:56 evidentemente eu só preparei depois que
13:58 os alunos tinham feito o mini teste e
14:01 entregado o mini teste, e aí no gabarito
14:03 Dá para ver que, bom... aqui é o eixo x,
14:07 aqui é o eixo y...
14:09 então o plano z=1 é o plano que
14:12 passa por aqui... essa linhas aqui estão
14:14 pontilhadas, essa linha daqui é a
14:16 interseção do plano z=1 com a nossa
14:19 figura...

14:20 a interseção com o plano x=1
14:25 é essa curva daqui,
14:27 a interseção com o plano x=3 é
14:31 essa, com x=4 é essa daqui,
14:38 etc...
14:40 e também tem uma interseção com
14:42 plano y=2.

14:45 Então, nos primeiros semestres da
14:48 pandemia os alunos ainda estavam
14:50 conseguindo fazer esse tipo de coisa
14:51 relativamente bem...

14:53 depois eles começaram a ter muita
14:55 dificuldade com isso. Algumas pessoas tinham
14:57 bastante facilidade com isso e outras
14:58 pessoas tinham uma dificuldade infinita que
15:00 eu não sabia como resolver, e eu não
15:02 sabia desmontar esse problema em vários
15:04 pedaços menores...

15:07 aí eu fui mudando esse problema pra
15:10 outros problemas em que quando os alunos
15:12 tinham dificuldade eu conseguia
15:16 desmontar o problema em vários para eles
15:19 conseguirem resolver tudo passo a passo...

15:21 Então teve um certo momento - no semestre
15:24 seguinte, 2021.1,
15:29 em que eu passei um exercício no qual a
15:32 superfície em que a gente tinha que
15:33 trabalhar era essa daqui...

15:35 repara que não é mais uma superfície
15:37 dada por uma equação simples...
15:39 uma fórmula simples, que os livros
15:43 costumam usar... a fórmula que dá essa
15:45 superfície aqui é uma fórmula que usa
15:46 máximos e mínimos, os livros não fazem isso,
15:49 os livros costumam evitar funções
15:52 definidas por casos... e aí eu tava de
15:55 propósito dando questões que
15:59 os livros não tratavam, os alunos iam ter que
16:02 aprender a trabalhar isso por chutar e
16:04 testar...

16:06 tinha toda uma metodologia pra isso,
16:08 mas não bastava os alunos ficarem
16:10 simplesmente procurando na internet onde
16:12 tem vídeo pra resolver questões
16:15 desse tipo porque ele não ia encontrar...
16:16 quer dizer, não sei, né, mas eu já tinha
16:19 procurado muito e nunca tinha encontrado
16:21 grande coisa sobre como resolver
16:23 questões desse tipo... então, uma das
16:26 superfícies que a gente ia trabalhar
16:28 nesses exercícios dava uma pirâmide, aqui...
16:31 e uma outra dava uma cruz.

16:36 aí eu fui melhorando esses exercícios um
16:39 pouco, e deixa eu mostrar umas figuras do
16:41 que que eu fui fazer... como é que isso foi
16:45 virando... que que isso virou no primeiro
16:48 semestre depois da pandemia...

16:52 eu passei a usar essas figuras aqui pra...
16:54 eu cheguei a fazer uma introdução
16:57 usando Minecraft para
16:59 mostrar que em alguns jogos a gente usa
17:02 figuras que são principalmente feitas de
17:04 polígonos, e no Minecraft muita coisa é
17:07 feita com figuras feitas de cubos...

17:09 e existe até um termo pra essas figuras
17:12 feitas de poucos polígonos - esse termo é
17:15 "Low Poly". Se você procurar na internet
17:18 por ele você encontra várias coisas sobre
17:20 essa estética de figuras feitas com
17:22 poucos polígonos. E a gente ia trabalhar
17:25 em superfícies
17:30 feitas de polígonos, feitas de poucos
17:32 polígonos...

17:34 e a gente ia aprender a
17:37 olhar pra um diagrama de numerozinhos,
17:40 entender que superfície era essa, e às
17:43 vezes esses diagramas de numerozinhos eram meio
17:44 ambíguos... por exemplo, nesse caso aqui
17:46 esse diagrama de numerozinhos dá
17:48 a altura dos pontos de
17:49 uma pirâmide, mas se a gente
17:53 fizer esse truquinho aqui, que eu já vou
17:55 mostrar em 3D...

17:57 a gente chega uma figura que tem
18:00 exatamente os mesmos númerozinhos, mas
18:03 que nesse cantinho daquele ela tem um
18:06 dente, a pirâmide tem um pedaço faltando...

18:09 Deixa eu ver se eu consigo
18:12 mostrar o vídeo... caramba, o vídeo está em
18:14 outro lugar, então vou mostrar ele num
18:16 ponto... num outro ponto desse vídeo eu
18:19 vou mostrar uma animação de uma figura
18:21 em 3D que mostra exatamente o que que
18:23 acontece nesse nesse lugar esquisito.

18:28 Agora deixa eu mostrar um outro slogan.
18:32 É uma outra história de Geometria
18:34 Analítica, só que essa é fictícia e essa é
18:36 recente. Essa eu só inventei há pouco
18:39 tempo atrás e eu ainda não apliquei nas
18:42 minhas turmas, vou começar a aplicar na
18:44 turma de Cálculo 2 desse semestre que vai
18:46 vir agora, 2023.1.

18:50 Então, é uma outra historinha sobre a
18:53 Geometria Analítica... lembrem que
18:56 em quase todas as minhas histórias em
18:58 que o Bob aparece as histórias terminam
19:01 com "Seja como o Bob"... e aí essa é uma
19:04 história de Geometria Analítica em que
19:05 os personagens são o Alex, o Bob o e Carlos...
19:08 deixa eu aumentar um pouquinho aqui - não,
19:10 deixa eu aumentar muito...

19:15 então,
19:16 nessa história daqui o Alex, o Bob e o
19:19 Carlos fizeram Geometria Analítica
19:21 juntos, e a última parte do curso era
19:24 sobre R^3, e um dos assuntos que ia cair
19:26 na prova dessa parte do curso era a
19:29 fórmula para calcular distância entre
19:31 duas retas...
19:32 o termo comum em português para isso é
19:35 "distância entre retas reversas".

19:39 E aí os livros que eles estavam usando
19:43 descreviam essa fórmula, e o Alex e o
19:46 Carlos "sabem", entre aspas, que o objetivo
19:49 de cada matéria de Matemática é fazer as
19:51 pessoas aprenderem certos teoremas... então
19:53 eles decoraram essa fórmula de distância
19:56 entre retas reversas, e tentaram aplicar
19:58 ela na prova...

20:00 O Alex até conseguiu, mas a questão que
20:03 caiu na prova tinha vários itens e cada
20:06 item usava letras diferentes da fórmula
20:07 que ele tinha que decorado, então ele
20:10 precisou adaptar a fórmula dele... ele
20:11 gastou um tempão com isso e ele só
20:14 conseguiu fazer um item dessa
20:16 questão, não conseguiu fazer os outros.

20:19 E o Carlos... ele tinha decorado dessa
20:21 fórmula, que é difícil, errado, e aí num
20:24 determinado pontos da prova em que ele
20:25 tentou aplicar a
20:27 fórmula que ele tinha decorado errado
20:32 ao invés de chegar num número
20:33 teve um ponto em que
20:35 as contas dele...
20:37 bom, pra poder continuar aquelas contas
20:40 ele ia precisar dividir um número
20:41 negativo por um vetor, e ele não sabia como
20:44 fazer isso... dica: NÃO DÁ.

20:49 E não só isso, como tanto o Alex quanto
20:52 o Carlos esqueceram a fórmula que eles
20:54 tinham decorado logo depois da prova.

20:57 Agora vamos pro Bob. A segunda coluna
20:59 é sobre o Bob.

21:03 O Bob estudou essa parte da matéria de
21:05 um outro jeito. Ao invés dele pensar "toda
21:08 vez que eu precisar calcular distância
21:10 entre duas retas e só usar a fórmula", ou
21:12 seja, ao invés dele sempre começar pela
21:14 fórmula, ele considerou que tem muitos
21:17 casos simples em que ele sabe calcular a
21:18 distância entre as retas no olhômetro...

21:21 Lembrem que aqui
21:29 eu discutia como a
21:32 gente fazer determinados exercícios
21:34 apontando para pontos em R^3 numa
21:37 numa estrutura de papel dessas
21:40 daqui, tá... então,

21:42 o Bob tinha uma certa prática com essas
21:44 coisas, ele sabia visualizar certas retas
21:46 muito simples muito bem, e aí ele sabia...
21:51 voltando para cá...

21:54 tem muitos casos simples em que ele, Bob,
21:57 sabia calcular a distância entre retas no
22:00 olhômetro - por exemplo o caso em que uma
22:02 das retas é paralela ao eixo y...

22:07 e aí a partir desses casos muito simples
22:09 ele foi aprendendo como lidar com vários
22:11 outros casos um pouco menos simples...

22:15 e aí
22:17 ele aprendeu a visualizar o que que
22:21 aquela fórmula complicadíssima
22:22 "quer dizer". Ele descobriu que
22:26 aquela fórmula calcula a altura de um
22:28 certo paralelepípedo - um pedaço da
22:30 fórmula cálcula o volume de um
22:31 paralelepípedo, um outro pedaço calcula a
22:34 área da base do paralelepípedo, e a
22:36 fórmula em si divide esse volume pela
22:38 base e calcula a altura do
22:40 paralelepípedo.

22:42 E aí o Bob tratou essa fórmula como algo
22:46 que generaliza vários casos simples que
22:48 ele entende bem, em que ele consegue
22:50 calcular distância entre duas retas por
22:52 outros métodos... e aí ele usou esses casos
22:55 simples para testar se a fórmula
22:57 realmente dava o resultado que ele
22:59 esperava.

23:00 Repara, ao invés dele confiar
23:02 automaticamente na fórmula ele foi
23:04 testando a fórmula em determinados casos
23:07 para ver se a fórmula realmente dava o
23:09 resultado que deveria dar... ele tinha uma
23:13 noção do que que a fórmula
23:14 deveria dar.

23:17 E aí isso aqui, esse pedaço aqui, é o que
23:20 virou o slogan da página. Mas primeiro deixa
23:23 eu ler esse parágrafo... tanto o Alex quanto o Bob
23:26 quanto o Carlos "estudaram pelo livro", mas
23:29 existem vários modos de "estudar pelo
23:31 livro", e o Bob usou modos que nem o Alex
23:34 nem o Carlos conheciam.

23:36 E aí: nesse curso - Cálculo 2 - você vai
23:39 aprender, e treinar, vários modos de
23:42 estudar pelo livro que provavelmente vão
23:45 ser totalmente novos para você.

23:48 Tá, então,
23:51 de vez em quando eu vou eu vou me
23:54 referir a isso aqui... tipo quando os alunos
23:56 acharem que basta decorar umas
23:58 fórmulas eu vou dizer "releia o slide
24:01 sobre retas reversas", ou vou repetir "em
24:05 Cálculo 2 você vai aprender vários modos
24:07 novos de estudar pelo livro
24:10 e treinar eles, e eles vão ser
24:12 completamente novos para você".

24:19 Tem umas idéias importantíssimas
24:22 escondidas aqui nesse parágrafinho mas eu
24:25 acho que eu vou voltar para elas depois, tá...
24:26 Por enquanto deixa eu só contar pra
24:30 vocês que vai ter mais coisa aqui.

24:34 Então, voltando...
24:40 um slogan que eu tenho usado muito nos
24:43 meus cursos é "Releia a dica 7".
24:47 Lembrem que... bom,
24:50 aqui tem um slide cujo título é
24:54 "Releia a dica 7", é que tem todas as
24:57 dicas que eu usava pra GA, mas eu já
25:00 dou bastante ênfase nessa dica 7 daqui...

25:06 E na verdade ele tem muitas, muitas, muitas
25:08 idéias aqui dentro. Dá pras pessoas
25:10 entenderem isso aqui superficialmente, e
25:12 aos pouquinhos eu vou mostrando que em
25:14 cada item daqui tem várias idéias
25:17 escondidas que você pode ir entendendo
25:19 aos poucos.

25:25 Tem um trecho daquele vídeo sobre aulas
25:27 por Telegram no qual eu falo sobre isso...
25:28 se vocês quiserem ver que trecho é esse
25:31 ele começa no 4:10, deixa eu mostrar
25:33 como ele aparece aqui na página...
25:36 tá aqui: "Eu transformei todo o material
25:39 que eu produzi pra Geometria Analítica
25:41 em uma coisa chamada Material Complementar
25:43 pra Geometria Analítica, blablablá"...

25:50 Bom, voltando...
26:01 então, voltando, peraí...
26:08 deixa eu comentar algumas coisas
26:12 sobre essa dica 7 que nem todo mundo
26:15 nota... aliás, que os alunos demoravam pra
26:18 entender. Essa dica 7 ela é incrivelmente
26:20 geral, ela funciona pra um monte de tipos de
26:24 pessoas... e lembrem que no outro vídeo eu
26:27 falava sobre
26:32 um professor que achava que um determinado
26:34 passo era óbvio, o aluno
26:37 que não entendia aquele passo, e aí o
26:39 professor dizia "esse passo é óbvio sim"...
26:41 aí eu contava várias versões dessa
26:43 história, e, algumas versões o aluno ia
26:45 para casa estudar e ele virava a pessoa
26:46 para quem aquele passo era óbvio.

26:49 Então, essa Dica 7 ela também tem várias
26:51 idéias sobre você virar outra pessoa.
26:53 Os personagens dela são personagens que
26:56 você pode virar, você pode tentar fazer o
26:59 papel deles de propósito num
27:01 determinado momento, e a primeira coisa
27:03 que eu quero comentar agora é o seguinte...

27:07 Nessa dica 7 eu
27:16 sugiro que você teste se uma solução sua
27:19 tá bem escrita submetendo ela a várias
27:21 pessoas. As pessoas dos itens (a) e (b) são
27:24 você mesmo logo depois você escrevê-la...

27:27 "releia e veja se ela está clara"... e
27:30 "você mesmo horas depois ou no dia seguinte,
27:32 quando você não lembrar mais do que você
27:34 pensava quando você a escreveu". E aí depois
27:37 tem alguns itens nos quais eu falo sobre
27:39 submeter o que você escreveu
27:42 a outras pessoas... as pessoas muito tímidas
27:45 elas vão ter muita dificuldade com esses
27:47 itens daqui - o item (c), em que você submete a
27:50 um colega que seja muito seu amigo, o item (d),
27:52 em que você submete pra um colega que seja
27:53 menos seu amigo... e o item (e) é o
27:56 monitor ou professor.

27:59 Eu próprio tinha muita dificuldade com
28:01 isso. Quando eu tava na graduação eu era
28:03 patologicamente tímido, então o que
28:05 acontecia era que eu relia as minhas
28:08 soluções centenas vezes até achar que eu
28:12 podia mostrar elas para alguém.

28:14 Então eu ficava muito aqui nos itens (a) e
28:18 (b), mas o objetivo desse processo
28:22 daqui é você se transformar numa pessoa
28:24 autônoma, que sabe vários modos de
28:27 estudar pelo livro e em quase todas
28:29 esses modos você vai ter que "chutar e
28:32 testar", no sentido de que você vai ter
28:34 que escrever a sua idéia e depois testar
28:36 a sua idéia para ver se ela tá clara
28:38 relendo e ela pensando sobre ela de várias
28:40 formas, e
28:42 em algum dia você vai chegar no ponto em
28:45 que você próprio consegue testar
28:47 praticamente tudo que você faz - mas até
28:49 lá é um longo processo...

28:52 então o objetivo é você chegar a ser a
28:55 pessoa que consegue resolver tudo
29:00 virando os personagens a e b - o
29:03 personagem que relê o que escreveu
29:05 logo depois de escrever e o personagem
29:07 que relê o que escreveu um tempo depois,
29:12 ou tendo esquecido os detalhes de
29:14 verdade ou tendo fingido que esqueceu os
29:16 detalhes e relendo aquilo como se você
29:18 fosse uma pessoa totalmente diferente da
29:21 pessoa que escreveu originalmente.

29:25 Voltando...
29:27 tem essa idéia daqui, de... repara:
29:30 o item (c) diz
29:34 "submeta a sua solução a um colega que
29:37 seja muito seu amigo", e o item (d) diz
29:38 "submeta a um colega que
29:42 seja menos seu amigo do que o outro".

29:44 Eu acabo citando isso em vários lugares.
29:47 Eu acabei não botando os links aqui, mas
29:50 tem vários lugares em que eu digo...
29:55 por exemplo alguém me mostrava uma coisa
30:01 e eu dizia: olha, eu não posso opinar
30:04 nisso aí porque eu só posso dizer que tá
30:07 bom se eu for fazer o papel do colega
30:09 muito seu amigo... o colega muito seu
30:12 amigo é o cara que relê a sua solução
30:15 50 vezes até ele entender, e aí ele diz:
30:18 ah entendi!...

30:21 o colega menos seu amigo ele vai ler o que
30:24 você escreveu e na hora ele vai dizer
30:26 "entendi" ou "não entendi"... ele não vai
30:28 tentar reler 50 vezes. E às vezes é
30:32 perigoso eu fazer o papel do
30:34 colega muito seu amigo porque se eu
30:36 fizer isso as pessoas vão achar que o
30:38 que elas escreveram tá bom, e aí quando
30:40 chegar na prova elas vão escrever
30:42 alguma coisa daquele jeito, e quando eu
30:46 der uma nota baixa e eu disser
30:48 "isso aqui tá muito difícil de entender",
30:49 "falta detalhe", e coisas assim, elas vão
30:52 dizer: mas professor, no dia tal você
30:54 disse que tava bom...

30:55 Então eu tomo muito cuidado com essa
30:58 história, em alguns momentos eu digo pros
31:00 alunos... caramba, eu devia ter posto os
31:02 links disso aqui, vou tentar botar os links
31:04 depois - links pra várias páginas em que
31:05 eu disse pros alunos: "olha, aqui eu não
31:08 posso fazer o papel do colega muito seu
31:09 amigo, tá?"

31:14 Mas na prova eles iam ter que saber que
31:18 eu ia ler as respostas deles não como
31:22 "colega muito seu amigo" mas como "colega
31:24 menos seu amigo", e eles tinham que ter
31:26 prática com isso.

31:28 Então o ideal mesmo é que quando você
31:32 faz esse exercício aqui de submeter o
31:34 que você escreveu a várias pessoas
31:36 você aos pouquinhos consiga fazer tanto
31:38 o papel da pessoa que é o colega muito
31:42 seu amigo quanto o papel da pessoa que é
31:45 um colega menos seu amigo. Mesmo quando
31:47 você próprio tá relendo a sua solução
31:51 você pode reler ela fazendo papel da
31:53 pessoa (c), o colega que é muito seu
31:55 amigo e você pode reler ela como uma
31:58 pessoa (d),
32:01 de uma forma mais benevolente, em que
32:04 você se dispõe a entender as coisas que
32:06 não tão claras, ou de uma forma muito
32:08 rigorosa, em que toda vez que você
32:11 encontrar algo que esteja ambíguo você
32:12 vai de propósito interpretar aquilo da
32:15 forma errada.

32:17 Então deixa só repetir de novo: o
32:20 objetivo disso aqui é você aprender a
32:22 fazer todos esses papéis.

32:26 Voltando...
32:29 aqui no final também tem uma outra coisa
32:32 que vai acabar sendo muito importante:
32:33 essa frase aqui, ó. Se as outras pessoas
32:37 acharem que ler a sua solução é um
32:39 sofrimento, isso é mau sinal; se as outras
32:42 pessoas acharem que a sua solução está
32:43 claríssima e que elas devem estudar com
32:45 você, isso é bom sinal.

32:48 Então repara que essa página aqui,
32:53 cujo título era "Releia a dica 7", ela
32:56 não termina com "Seja como o Bob!". Na verdade
32:59 aqui os personagens nem tem nomes, mas o
33:03 objetivo é você virar a pessoa...
33:06 essa pessoa daqui: a pessoa que as outras
33:09 pessoas...
33:10 elas acham que vale a pena estudar com
33:12 você.

33:16 Voltando...
33:25 eu vou ter que voltar para várias coisas
33:26 que eu já mostrei depois tá, mas deixa eu
33:29 apresentar um montão de idéias antes...
33:30 depois vou tentar conectar elas aos
33:33 pouquinhos.

33:35 Deixa eu fazer alguns comentários sobre
33:37 uma questão que que era muito importante
33:40 em Cálculo 2,
33:42 e num determinado semestre eu dei
33:45 não me lembro se foi um mini-teste ou
33:47 uma prova sobre ela, e os alunos se deram
33:49 catastroficamente mal...

33:51 Era o seguinte. Os alunos costumam achar
33:54 que basta eles decorarem determinadas
33:56 fórmulas e teoremas, né?
33:58 Então muitos alunos decoram a fórmula do
34:01 Teorema Fundamental do Cálculo
34:08 e eles acham que eles podem aplicar
34:10 aquilo em tudo, e tem determinadas
34:12 situações em que se eles aplicarem aquela
34:14 fórmula dá um resultado errado...

34:18 Então teve um semestre que eu dei uma
34:22 questão
34:26 em que se eles calculassem a área de uma
34:29 determinada coisa usando o Teorema
34:31 Fundamental do Cálculo dava um resultado
34:33 ERRADO, e se eles calculassem aquilo
34:35 fazendo o desenho eles chegavam no resultado
34:37 certo, e
34:40 muitos alunos chegavam a resultados em que
34:43 eles simplesmente diziam no final:
34:44 "então 3=4!"

34:49 E aí eu vi que nenhum aluno... não, não; ou
34:54 nenhum aluno ou só um aluno teve coragem de
34:56 escrever algo tipo "esse resultado tá
34:57 errado, mas eu não sei porquê".

35:00 Eles achavam que eles tinham que
35:03 escrever tudo em tom de certeza.

35:08 Uma das idéias que está escondida aqui
35:10 na dica 7 é o seguinte.

35:14 Primeiro deixa eu voltar a uma idéia
35:17 que eu contei no outro vídeo. No outro
35:19 vídeo eu falava muito sobre passos
35:23 que são óbvios e passos que são óbvios pra
35:26 pessoas que estão num determinado nível
35:28 mas não são óbvios pra pessoas
35:31 que estão num nível abaixo, e eu falava que
35:34 quando a gente aprende a ler textos de
35:37 matemática em voz alta bem
35:39 a gente consegue sinalizar no tom com que
35:42 a gente tá lendo o que que é mais óbvio, o
35:43 que que é menos óbvio, qual é o nível de
35:46 dificuldade de cada passo, e coisas assim.

35:49 Se as pessoas exercitam muito essa dica
35:51 7 de estudar junto com os colegas e
35:53 fazer vários papéis
35:56 elas acabam aprendendo a sinalizar uma
35:58 outra coisa que é super importante, que é
36:01 GRAU DE CERTEZA. Se elas estão estudando
36:03 junto com uma outra pessoa algo que
36:06 que elas estão descobrindo aos poucos
36:09 elas vão conseguir sinalizar algo tipo
36:12 "esse passo aqui é claríssimo e eu sei
36:15 explicar os detalhes" e tem um outro
36:17 passo que elas vão usar outro tom de voz
36:18 para dizer "eu acho que é desse jeito".

36:23 E quando os alunos fizeram essa questão
36:25 sobre o TFC2 e chegaram a 3=4
36:28 nenhum desses alunos conseguia indicar
36:34 que aquele passo tava esquisito, que
36:36 ele passo tava errado.

36:37 Deixa eu mostrar
36:38 como é que é essa questão se transformou
36:40 com o tempo. Teve uma prova em que eu
36:43 avisei que eu ia dar uma questão sobre
36:45 o TFC2, e eu até disse para eles
36:48 consultarem as versões anteriores dessa...
36:52 de questões parecidas com aquilo, e
36:56 nessa prova o que eu dei foi o seguinte...

36:59 Isso aqui é o gabarito da questão 3,
37:01 deixa eu voltar pro enunciado da
37:04 questão 3... eu dei a questão desse jeito.

37:09 Deixa eu dar um zoom aqui...
37:13 Nesse semestre eu tava... pra cada teorema eu
37:16 tava separando a fórmula do teorema e as
37:19 hipóteses do teorema, e eu avisava pros
37:22 os alunos que às vezes quando as
37:23 hipóteses não forem cumpridas a fórmula
37:25 vai dar resultados errados, e eu também
37:27 tava dando nomes pras fórmulas.

37:30 Então isso aqui é a fórmula do TFC2, e eu
37:34 disse: mostre que quando a, esse limite
37:37 de integração daqui, é 1, e b, que é esse
37:40 limite de integração daqui, é 3, e
37:42 quando a função F é essa daqui,
37:44 a fórmula [TFC2] dá um resultado falso.

37:49 E aí eu dou umas dicas, e aí
37:52 o gabarito dessa questão
37:56 é isso aqui...
38:00 o gráfico da função F é esse,
38:03 o gráfico da derivada da F é esse aqui,
38:06 o que a gente precisava calcular era
38:09 uma integral dessa derivada daqui
38:13 e aí a integral dava essa áreazinha daqui...

38:18 E aí aqui eu uso esses "\underbrace"s pra
38:21 indicar resultados parciais, e essa área
38:25 daqui dava 3 - dá para ver pelo desenho...
38:29 se a gente calcula
38:31 isso aqui pelo operador de diferença a
38:35 gente obtém 5, então
38:38 essa igualdade aqui tá dizendo que 3=5,
38:40 mas a gente vai tratar ela
38:42 como uma comparação, e o resultado dessa
38:44 comparação daqui é falso - 3=5 dá falso.

38:53 Bom, deixa eu só mencionar uma coisa
38:56 rapidinho... eu tenho feito os gabaritos de
38:58 forma que eles acabam sendo muito úteis
39:01 depois para discutir modos de escrever.

39:06 Tá, mas deixa eu voltar.
39:11 uma outra coisa que eu tenho apresentado
39:12 nos cursos é o seguinte.

39:20 Se alguém quiser ver como eu apresentei
39:22 isso naquelas legendas do "Sobre aulas por
39:25 Telegram" esse trecho começa no 33:31.
39:28 Deixa eu abrir a página aqui...

39:33 Eu falei um pouquinho sobre como é que
39:35 eu apresentava em Cálculo 2
39:36 que expressões matemáticas tinham que ser
39:41 interpretadas como árvores, e o Carlos
39:44 Tomei, que era o organizador dessas
39:47 reuniões por Zoom, ficou empolgadíssimo...

39:52 Mas voltando...
39:55 eu aos pouquinhos fui desenvolvendo
39:58 modos cada vez melhores de apresentar essa
40:00 ideéia de que a gente vai tratar
40:02 expressões matemáticas como árvores...
40:07 aqui tem um pointer pra um quadro do
40:10 último semestre...

40:11 então, no quadro eu usava
40:13 essas figurinhas daqui... eu começava
40:16 mostrando que árvores normalmente são
40:17 são representadas desse jeito,
40:27 assim, com bolinhas...

40:36 mas os programas que eu tava usando iam
40:39 representar árvores de um outro jeito que era
40:41 muito mais fácil de fazer em ASCII...
40:42 então a gente tinha que imaginar que
40:45 essa árvore é transformada numa árvore
40:46 desse tipo daqui simplesmente porque é
40:48 muito mais fácil fazer um programa para
40:50 desenhar isso do que fazer o programa
40:52 para desenhar as bolinhas chiques.

40:55 E aí no último semestre eu já tinha
41:00 algumas figuras para isso...
41:04 eu fiz um programa...
41:08 umas funções do Maxima que pegavam
41:11 expressões do Maxima e mostravam a
41:13 representação em árvore delas.
41:15 Deixa eu ver se eu consigo mostrar...

41:20 Aqui.
41:24 Então MV2 era uma determinada fórmula
41:27 na sintaxe do Maxima... primeiro eu defino
41:31 ela e depois o Maxima representa ela na
41:33 notação 2D preferida dele, e aí eu rodava
41:35 o meu programinha pra mostrar como era a
41:37 representação interna disso aqui
41:39 em árvore, e as pessoas viam que a
41:43 representação interna
41:44 era essa... essa integral daqui virava uma
41:46 operação "integrate", que tinha quatro
41:49 argumentos, o primeiro argumento era o
41:52 que tava dentro da integral, o segundo
41:54 era a variável de integração e os outros
41:56 dois eram os limites de integração...

42:01 o operador central disso aqui era uma
42:04 igualdade, então
42:07 o lado esquerdo da igualdade era essa
42:09 integral daqui, e o lado direito da
42:11 integral era isso aqui...

42:13 e durante a aula os alunos até me
42:15 perguntavam qual era a representação em
42:17 árvore de determinadas coisas, e eu rodava
42:19 isso no Maxima na hora e mostrava qual
42:22 era o resultado.

42:23 E eu também mostrei pra eles que se você
42:25 pega um outro programa de computação
42:27 simbólica, por exemplo o SymPy...
42:32 o SymPy usa uma representação interna
42:35 um pouco diferente...
42:39 peraí, deixa eu ver se eu consigo dar
42:41 zoom nisso...
42:43 consigo, mas fica meio feinho...

42:47 essa expressão daqui, x^x + 42,
42:50 virava isso... até aqui nada de muito
42:53 extraordinário, a não ser que a soma
42:55 virou "Add" e a potência virou "Pow"...

43:02 E aí essa
43:07 essa soma daqui, de f(x) com uma
43:09 determinada derivada, virava essa coisa
43:12 esquisita daqui... na verdade isso aqui é
43:14 uma segunda derivada...

43:15 Então com isso os alunos entendiam que
43:20 cada programa usa uma representação em
43:22 árvore diferente, e quando a gente lê um
43:25 livro de matemática a gente não tá vendo
43:27 qual é a representação em árvore por trás...

43:29 Às vezes a gente vai ter que improvisar um
43:30 pouco, a gente vai ter que fazer uma
43:31 hipótese, e pode ser que a nossa hipótese
43:34 seja tão boa quanto a do nosso colega, e
43:37 outro colega tenha feito uma outra hipótese
43:39 totalmente diferente de como
43:42 representar determinadas coisas em
43:44 árvore.

43:46 Aqui também tem
43:49 algumas coisas que eu usei nesse
43:51 exercício do último semestre...
43:54 deixa eu ver...

44:00 Eu também mostrei que
44:06 tem determinadas as coisas que a gente
44:07 não pode escrever porque elas não têm
44:09 representação em árvore - por exemplo
44:12 dy/dx vai ter uma representação
44:16 em árvore, porque é uma derivada, mas dx
44:20 sozinho não tem...

44:22 e, pior ainda, vai ter um
44:24 determinado momento do curso em que...
44:28 deixa eu mostrar o slide disso aqui...

44:32 eu falo sobre a linguagem de Cálculo 2
44:35 e eu digo isso aqui, ó...

44:39 primeiro - primeira péssima notícia:
44:44 nenhum livro define precisamente a
44:47 gramática da linguagem de Cálculo 2.
44:49 você vai ter que deduzir qual é a
44:51 gramática, qual é a linguagem válida,
44:53 lendo os livros do curso... não é que nem
44:56 C em que tem um apêndice no qual você tem
44:58 a descrição em BNF de qual é a linguagem.

45:00 A linguagem de Cálculo 2
45:02 você vai ter que meio que adivinhar ela,
45:04 vai ter que deduzir qual é ela...
45:07 então você vai ter que fazer as suas
45:10 hipóteses, vai ter que chutar e testar
45:11 bastante, e discutir com seus colegas,
45:13 e comigo e com o monitor.

45:16 E péssima notícia número 2:
45:18 Cálculo 2 não tem uma linguagem só,
45:20 tem várias! Em alguns momentos do curso
45:23 a gente vai permitir a notação de Leibniz,
45:25 na qual a gente pode falar de dx e dy
45:28 sozinhos, e em outras partes do curso
45:32 isso vai ser proibido...

45:34 e a gente vai ter que considerar que
45:36 Cálculo 2 tem duas linguagens
45:37 diferentes, e às vezes pra conseguir
45:39 interpretar formalmente a linguagem com
45:41 a notação de Leibniz a gente vai ter que
45:44 traduzir ela pra notação na qual
45:47 certas operações são proibidas.

45:54 Aqui tem um link pro exercício das
45:56 árvores... deixa eu ver...
46:02 ah, isso aqui é simplesmente aquele
46:04 exercício em que tinha uma foto do
46:07 quadro que eu mostrei agora há pouco,
46:08 exceto que aqui eu falo do Macaco
46:11 Derivador. É o seguinte. Eu comecei o
46:14 curso mostrando um vídeo do Mathologer
46:17 sobre um livro chamado "Calculus Made Easy".
46:20 E aí ele diz que derivar é uma coisa tão
46:24 fácil que você pode treinar um macaco
46:26 para derivar... e na verdade esse
46:29 Macaco Derivador é um programa. A gente
46:31 pode definir um programa que calcula
46:33 derivadas, e isso é
46:35 relativamente fácil...
46:38 E aí eu usava muito essa expressão do
46:40 Macaco Derivador, tá.

46:44 Aqui tem uns comentários sobre
46:47 árvores... tem esse muito
46:50 importante daqui, que eu usava como
46:52 slogan... às vezes eu apontava para isso e
46:54 dizia "releia o slide 11"... eu dizia:
46:58 lembre que na maior parte do curso
46:59 a expressão `dx' não vai poder aparecer
47:01 sozinha...
47:04 e eu
47:07 muitas vezes eu vou me referir ao dx
47:10 como uma espécie de "fecha parêntese",
47:12 então numa integral o sinal de integral
47:14 funciona como um abre parêntese e o dx
47:17 funciona como fecha parêntese, e se você
47:20 tem algo como f(x) dx
47:22 é como se você tivesse uma
47:25 expressão que tem um fecha parêntese e
47:27 não tem o abre parêntese correspondente...
47:30 e isso aqui virou um slogan que eu repetia
47:32 muitas vezes.

47:36 Deixa ver se tem algum... ah, achei.
47:39 isso aqui é uma coisa que eu tava
47:41 devendo.
47:45 Eu mostrei para vocês uma figurinha de...
47:47 da pirâmide em que a gente tirava um
47:49 pedaço dela. Eu discuto isso num
47:53 vídeo chamado "cabos na diagonal".
47:57 Se a gente assiste um pedacinho do
48:00 vídeo...

48:18 Tá? Então era difícil construir essa figura
48:20 em papel, mas quando eu mostrava essa
48:22 animação em 3D as pessoas entendiam o
48:24 que que era aquilo.

48:26 E também tem um outro vídeo...
48:29 aliás, tem outro trecho daquele outro
48:31 vídeo em que eu tava discutindo o
48:33 exercício da pirâmide, e eu tava
48:34 mostrando pros alunos como é que a
48:36 gente podia calcular a altura
48:38 de pontos com coordenadas não inteiras
48:40 de vários jeitos...

48:42 Se você já tivesse uma intuição
48:44 visual boa suficiente você entenderia
48:46 que em todos esses pontos daqui
48:48 a altura é 0.5...
48:51 a altura daqui tava dada explicitamente no
48:54 diagrama de numerozinhos - era 0 - a daqui
48:57 também, a daqui também... mas a gente tinha
49:00 que usar outras técnicas para descobrir
49:02 que a altura daqui era 0.5...

49:04 E aí tinha várias técnicas.
49:07 A técnica mais óbvia é a gente usar a
49:10 definição da função que dá a superfície
49:12 dessa pirâmide, que é uma função
49:14 com máximos e mínimos, e calcular por
49:16 força bruta qual é a altura desses
49:18 pontos daqui... por exemplo, esse ponto
49:20 aqui tem coordenadas x=2.5 e y=2.5,
49:22 e se a gente fizer as contas todas
49:26 a gente descobre
49:28 que o z desse ponto é 0.5 também.

49:35 E eu usava isso pra fazer os alunos
49:38 começarem a ter intuição visual
49:42 de situações em que a gente varia uma
49:45 quantidade - por exemplo, a coordenada x -
49:49 e a gente vê como uma outra quantidade
49:51 varia em consequência dessa -
49:53 a coordenada z.

49:56 Daqui a pouco eu vou mostrar mais
49:58 figuras sobre isso, tá...
50:03 mas deixa eu ir apresentando as coisas
50:05 na ordem das minhas anotações aqui...

50:07 Tinha uma outra coisa que teve que virar
50:10 um slide porque se eu não transformasse
50:12 aquilo em slide os alunos iam
50:16 entrar em parafuso com aquela idéia,
50:18 porque é uma idéia complicada...

50:21 Numa das primeiríssimas aulas de
50:27 Cálculo 2 desse último semestre
50:31 eu tava apresentando Somas de Riemann...
50:33 oops, desculpa, não era uma das primeiras
50:37 não... mas a gente voltava à idéia de medir
50:44 áreas no olhômetro, a gente interpretava
50:47 determinadas figuras feitas de
50:49 retângulos, a gente dividia as figuras em
50:52 vários retângulos separados e calculava
50:54 a área de cada pedacinho retangular.

50:57 E aí a gente representava os nossos
50:59 retângulos nessa forma daqui.
51:03 Nossos retângulos eram representados como
51:05 altura vezes base - aqui a extremidade
51:08 direita e aqui a extremidade esquerda.
51:10 Então a gente ia interpretar isso aqui como
51:12 um retângulo...
51:14 se a gente interpretasse isso aqui como um
51:17 número a gente perdia a informação de
51:19 qual era a extremidade esquerda e
51:21 a extremidade direita, e se além disso a
51:23 gente multiplicasse isso aqui por isso
51:25 aqui a gente perdia a informação de
51:27 qual era a altura do retângulo.

51:29 Então na maior parte do tempo
51:31 valia a pena a gente pensar nisso aqui
51:33 como uma expressão - em árvore -
51:35 na qual o lado esquerdo dessa
51:37 multiplicação é a altura e o lado
51:39 direito é a base, e nessa base aqui o
51:43 lado esquerdo da subtração é a
51:46 extremidade direita e o lado direito é a
51:49 extremidade esquerda.

51:52 E aí quando a gente pensa em retângulos
51:57 como expressões desse tipo
52:01 a gente começa a ver que alguns desses
52:05 números podem ser negativos...

52:07 Aí aqui tem uma descrição de como
52:09 interpretar isso geometricamente...

52:12 E aí isso aqui é importantíssimo.
52:18 Se eu não tivesse um slide disso eu tava
52:21 ferrado, tá... mas como eu tinha o slide
52:24 eu podia pedir pros alunos relerem isso
52:26 várias vezes. Foi MUITO útil.

52:29 Então, deixa eu ler isso aqui pra vocês.
52:31 Lembre que matemáticos e físicos pensam de
52:33 jeitos muito diferentes. Por exemplo, é
52:35 comum livros de Física dizerem coisas
52:37 tipo "áreas negativas não existem! Então
52:39 temos que fazer o ajuste tal!" ou "a massa
52:42 não pode ser negativa", e não sei quê...
52:44 mas é comum livros de Matemática dizerem
52:46 coisas tipo "vamos supor que existe um
52:49 número i tal que i^2 = -1"...

52:54 Então eu preparava tudo isso
52:56 e depois a gente ia até levando isso
52:58 pra lugares mais interessantes, a gente
53:00 discutia retângulos degenerados,
53:03 círculos degenerados, e coisas assim,
53:06 e alguns dos nossos retângulos tinham
53:08 áreas negativas.

53:15 Aqui tem um link pro material sobre
53:17 retângulos degenerados...

53:20 Aqui tem vários exercícios de "interprete
53:23 essas coisas aqui como retângulos"...
53:25 "esses dois retângulos aqui tem a mesma
53:26 interpretação geométrica mas um tem área
53:28 positiva e o outro tem área negativa"...

53:32 E a partir do momento que os alunos se
53:34 a costumavam com isso muita coisa em
53:37 propriedades da integral
53:39 ficava muito mais fácil...

53:42 eu até pedia para eles lerem
53:46 uma determinada página da Wikipédia
53:49 sobre figuras degeneradas...

53:53 e isso aqui era minha versão dessa idéia
53:56 do semestre anterior. Então aqui tinha
53:59 vários links pra Wikipedia...

54:07 Então, repara: eu tava produzindo todo
54:10 esse material sobre dúvidas comuns
54:12 dos alunos e esse material tava sendo
54:15 incrivelmente útil pra mim.

54:19 Deixa eu voltar para uma coisa
54:24 da minha apresentação sobre aulas por
54:30 Telegram? A minha apresentação foi na
54:34 na terceira reunião de uma determinada
54:37 série... se a gente vier para essa página
54:39 aqui do "Sobre aulas por Telegram"...
54:43 não, a minha foi na quarta.

54:46 E na reunião 2 um cara chamado Henrique
54:49 Sá Earp fez uma apresentação sobre o que
54:51 ele tava tentando fazer pras pessoas
54:53 compartilharem mais material...
54:55 e teve um ponto da minha apresentação
54:57 em que ele fez um comentário muito bacana.

55:00 Então, voltando.
55:01 Eu terminei a minha apresentação
55:03 dizendo o seguinte:
55:13 eu falei que eu tive que adaptar
55:16 o meu jeito de dar aula
55:19 pras minhas limitações, falei como cada
55:22 pessoa do meu departamento tava
55:24 tentando fazer uma coisa diferente, e...
55:30 bom, não vou ler isso aqui em voz alta,
55:32 mas o negócio é que eu terminei a minha
55:36 apresentação
55:40 com uma espécie de pedido de desculpas.

55:45 Eu terminei ela com isso aqui, ó. Eu fiquei
55:48 morrendo de vergonha de 1. não ter coberto
55:50 uma parte da matéria e 2. ter aprovado um
55:53 monte de gente que colou, MAAAS talvez eu
55:56 tenha conseguido preparar um material
55:57 didático de Cálculo 2 e Cálculo 3 que seja
56:00 útil pra outras pessoas e que corresponda
56:01 a dificuldades que outros professores também
56:03 estão tendo...

56:07 Com esse material problemas que os
56:09 alunos levaram quatro aulas pra
56:10 resolver dessa vez porque eu tive que
56:13 preparar um montão de
56:15 sub-exercícios, dicas, vídeos, etc,
56:17 talvez virem exercícios que vão tomar
56:19 menos de uma aula no semestre que vem...

56:20 Então à medida que eu preparo esse material
56:22 eu vou conseguindo cobrir cada vez mais
56:28 material nos meus cursos...

56:31 e, talvez eu, que ando com habilidades
56:34 sociais bem ruins, consiga criar uma rede
56:36 de pessoas que estão trabalhando juntas -
56:38 pelo menos no sentido de usar com
56:40 frequência material uns dos outros,
56:42 e não sei quê...

56:44 E aí eu apresentei isso
56:45 e o Henrique Sá Earp fez um
56:50 um comentário a respeito do que ele
56:53 tinha apresentado na reunião 2... na
56:55 reunião 2 ele fez uma apresentação sobre
56:59 sobre como é que ele tava criando um
57:01 grupo, aliás, uma pasta no Google Drive,
57:03 em que qualquer pessoa registrada podia
57:07 entrar e colocar seu material lá...

57:11 A iniciativa é fantástica mas acabou não
57:14 dando muito certo, e eu acho que não deu
57:16 muito certo porque cada pessoa tá
57:17 acostumada com ferramentas diferentes...

57:21 Então as outras pessoas ficavam sem jeito
57:23 de usar isso, ficavam sem jeito de
57:26 alterar uma coisa que já parecia
57:27 arrumadíssima, a gente ficava com
57:29 vergonha de botar nossas coisas lá, e a
57:31 gente depois descobriu que a gente
57:34 também não tinha nenhum modo bom de ver
57:35 o que que tinha sido alterado
57:36 recentemente.

57:38 E aí depois a gente fez algumas
57:40 tentativas de criar outros modos de
57:43 compartilhar material. Nenhuma delas deu
57:45 muito certo, mas naquela época a gente
57:47 pelo menos estava tentando...

57:53 Deixa eu ir apresentando mais umas
57:55 coisas daqui, que tavam na ordem
57:58 dessas anotações meio caóticas daqui...

58:04 Lembrem que eu comentei, já em vários
58:07 lugares, que eu uso muito uma determinada
58:09 operação de substituição que tem me
58:12 ajudado muito porque quando os alunos não
58:13 sabem fazer uma operação que para eles é
58:16 difícil eu divido essa operação em
58:18 vários passos e aí eles conseguem
58:20 entender...

58:22 Tem momentos em Cálculo 2
58:25 em que a gente precisa usar somatórios...
58:29 E aí pra gente calcular esse
58:31 somatório daqui a gente tem que
58:33 pegar várias cópias dessa expressão
58:36 daqui, que tá dentro do somatório...

58:38 na primeira cópia o i vai virar 4,
58:39 na segunda o i vai virar 5,
58:40 na terceira o i vai virar 6,
58:41 e na quarta o i vai virar 7...

58:46 E aí dá para a gente fazer isso passo a
58:48 passo. Aqui tem as cópias, aqui tem as
58:49 instruções do que que o i vira, e no passo
58:52 seguinte a gente tem a versão em que o i
58:56 já virou 4, 5, 6 e 7.

59:02 Os alunos tinham muita dificuldade com
59:06 somatório e com várias outras coisas, e
59:09 essa operação de substituição acabou me
59:11 ajudando muito...

59:12 e deixa eu só comentar de novo que
59:16 em 2022.1 eu fiz uma coisa que foi
59:19 catastrófica. Como os alunos não sabiam
59:22 nem pegar uma fórmula simples
59:26 e transformar ela num caso particular no
59:29 qual o a era substituído por 3 e o b era
59:32 substituído por 4 - essa operação era
59:34 totalmente alienígena pra eles - eu
59:36 comecei a tentar insistir nessa
59:38 operação de substituição... e eu comecei a
59:41 preparar um bocado de material sobre
59:42 isso, e eu descobri que essa operação na
59:45 verdade ela é mais complicada do que
59:47 parece, ela tá cheia de corner cases, a
59:51 definição correta dela é super trabalhosa...

59:53 então eu comecei a preparar um material
59:55 sobre isso que ficou incompleto, que não
59:57 ficou fácil de entender, eu gastei tempo
59:59 demais com isso... foi uma catástrofe, tá.

1:00:02 Só no semestre seguinte eu aprendi um
1:00:05 bom jeito de explicar essa operação de
1:00:08 substituição pras pessoas, que era eu
1:00:11 dizer pra elas o seguinte...

1:00:18 Eu explicava pras elas que vai
1:00:20 ter um lugar que o curso tem um buraco...
1:00:21 na verdade tem vários, mas eu tinha que
1:00:25 explicar essa operação de substituição
1:00:29 meio pela tradução dela em português
1:00:31 meio por um montão de exemplos, mas eu
1:00:34 não ia poder explicar ela pela definição
1:00:36 formal dela porque só pessoas
1:00:40 muito mais experientes, que já
1:00:43 têm hábito de lidar com definições
1:00:45 recursivas, iam saber entender essa
1:00:48 definição formal...

1:00:52 Então eu ia mostrar pros alunos um monte
1:00:54 de exemplos de como é que essa operação
1:00:55 tem que funcionar,
1:00:57 tanto com essa notação mesmo
1:01:00 quanto com a versão dela em português,
1:01:02 e ia dizer: olha aqui vocês vão ter que
1:01:05 entre "usar o bom senso de vocês"
1:01:08 para entender qual o resultado
1:01:10 "que tem que dar"...

1:01:12 E aí tem um monte de critérios para isso.
1:01:16 Por exemplo, se você tiver um teorema e
1:01:18 você pegar um caso particular desse
1:01:19 teorema... todos os casos particulares de
1:01:22 um teorema têm que ser verdade.

1:01:24 Então eu dava alguns truques e eu dizia:
1:01:27 olha, infelizmente
1:01:30 antigamente no ensino médio as pessoas
1:01:32 treinavam isso durante centenas de horas
1:01:35 usando só a notação em português...
1:01:37 e aí elas se acostumavam com a idéia
1:01:40 de como é que essa substituição
1:01:42 "tem que funcionar"...
1:01:43 agora vocês vão ter que correr, tá...
1:01:47 se vocês ainda não treinaram essas centenas
1:01:49 de horas comecem a treinar, e me peçam ajuda
1:01:52 pra otimizar o tempo de vocês.

1:01:56 Deixa eu voltar um pouquinho pra
1:01:58 idéia de que a gente estava tentando
1:01:59 aprender a lidar com quantidades que
1:02:02 variam juntas.

1:02:08 Aqui tem um outro vídeo que eu fiz
1:02:11 sobre o problema da pirâmide.
1:02:14 Aqui tem até um desenho... que tá errado,
1:02:16 tá... caramba, esse tracinho deveria
1:02:18 ter ido um pouquinho... uma unidade
1:02:19 aqui atrás... putz, que vergonha!
1:02:24 o som dele tá horrível, mas tem legendas.

1:02:42 Então, nesse vídeo eu tou mostrando pros
1:02:45 alunos que quando a gente tem segmentos
1:02:48 de reta a gente tem uma noção...
1:02:51 a gente consegue deduzir
1:02:53 muito facilmente o quanto o y tem que
1:02:57 variar quando o x varia de uma
1:02:59 determinada forma... então aqui a gente tem
1:03:01 um coeficiente angular -1, e quando
1:03:03 o x aumenta 0.1 o y diminui 0.1.

1:03:09 E aí a gente tem que aplicar isso a
1:03:11 R^3 também. E eu comecei dando uns
1:03:14 uns exercícios difíceis, em que
1:03:19 eles tinham que pegar o problema da
1:03:21 pirâmide e ver o que que acontecia
1:03:22 quando x varia 0.1... algumas pessoas já
1:03:26 tinham essa noção de quantidades que
1:03:28 variam juntas e tinham bastante intuição
1:03:30 visual sobre isso, mas algumas pessoas não
1:03:32 tinham noção nenhuma disso, e tinham que
1:03:35 fazer horas de contas... e as contas com
1:03:38 0.1 são mais difícil do que as contas
1:03:40 com 0.5, que por sua vez são mais difíceis
1:03:44 do que as contas com números inteiros.

1:03:45 Então eu fui adaptando esses problemas pra
1:03:48 eles terem sempre versões em que as
1:03:51 contas são muito simples e depois a gente
1:03:53 poder passar para contas um pouquinho
1:03:54 mais complicadas.

1:03:56 E isso é uma tentativa
1:03:58 de fazer uma coisa que os livros fazem a
1:04:01 beça - mas de um jeito que os alunos
1:04:03 estavam com muita dificuldade.

1:04:11 Eu tentei trabalhar com os alunos
1:04:19 aquele livro chamado "Calculus Made Easy",
1:04:22 que é um livro do início do século 20,
1:04:24 que o autor se chama Silvanus Thompson,
1:04:26 e que eu também trabalhei
1:04:33 um vídeo do Mathologer sobre esse livro...

1:04:35 Então: o Mathologer fala maravilhas
1:04:38 desse livro, um monte de gente fala
1:04:40 maravilhas desse livro, e aí a gente ia
1:04:43 trabalhar alguns trechinhos desse livro,
1:04:46 e também vários livros em português.

1:04:50 Então,
1:04:52 a gente trabalhou um dos primeiros
1:04:54 exemplos desse livro, em que a gente tem
1:04:56 uma escada encostada numa parede, e o
1:05:00 Silvanus Thompson começa a analisar o que
1:05:02 que acontece se a gente puxa a base da
1:05:05 escada um pouquinho para fora...

1:05:08 ele chama essa distância entre a base da
1:05:12 escada e a parede de x e a distância
1:05:15 entre o chão e o topo da escada de y, e
1:05:19 ele considera dois momentos, x0 e x1...

1:05:22 E aí quando a gente chama esses momentos
1:05:24 de "antes" e "depois", de "momento 0"
1:05:28 e "momento 1", aí a gente consegue falar
1:05:30 de dx, e a gente consegue definir dx como
1:05:33 sendo x1-x0...

1:05:35 Na verdade ele nem usa x1 e x0,
1:05:37 ele fala em "antes" e "depois".

1:05:40 E aí eu fui dando as dicas de como é que
1:05:44 a gente podia traduzir a apresentação
1:05:45 dele para algo mais moderno, em que a
1:05:48 gente podia colocar o antes e o depois
1:05:50 um do lado do outro, e se a gente usasse
1:05:54 essa notação, com x0 e x1, ficava muito
1:05:57 mais fácil comparar o antes e o depois
1:05:58 e falar do antes e do depois ao mesmo tempo.

1:06:03 Quando a gente acessa isso no próprio
1:06:05 livro do Silvanus Thompson você tem essa
1:06:08 figura daqui e muita coisa em texto...

1:06:11 E aí eu tentei trabalhar os livros, tanto
1:06:13 o do Silvanus Thompson quanto o livro do
1:06:15 Daniel Miranda,
1:06:18 em que eles falavam de quantidades
1:06:21 variando juntas e essas quantidades não
1:06:23 eram exatamente infinitesimais, eram
1:06:25 simplesmente quantidade muito pequenas...

1:06:27 Então, nesse exemplo do Silvanus Thompson
1:06:31 as medidas são em polegadas e
1:06:35 ele analisa o que que acontece quando
1:06:37 essa distância daqui varia de uma
1:06:39 polegada. Então nesse momento inicial
1:06:42 pra ele fazer tudo de uma forma muito
1:06:44 concreta o dx não é um infinitesimal
1:06:46 de verdade, é
1:06:47 simplesmente um número muito pequeno... e
1:06:50 ele tá usando um truque que pra algumas
1:06:52 pessoas é naturalíssimo e pra
1:06:54 outras pessoas é
1:06:58 muito difícil de acreditar, que é que
1:07:01 quando o dx é muito pequeno
1:07:03 a gente vai poder linearizar as nossas
1:07:05 contas...

1:07:07 O que eu vi quando eu tava na faculdade
1:07:09 era que para
1:07:11 pessoas com "cabeça de físico" isso é
1:07:13 absolutamente natural e pra pessoas com
1:07:16 "cabeça de matemático" isso era um milagre
1:07:18 complicadíssimo que a gente precisava de
1:07:20 muita justificativa para poder entender
1:07:24 e usar...

1:07:27 Então, a gente tentou trabalhar isso...
1:07:30 tentou traduzir o modo como os livros
1:07:33 apresentam isso pra contas...
1:07:38 cadê? Deixa eu ver...

1:07:41 nessa página daqui tem essas figurinhas,
1:07:46 e na página seguinte...
1:07:49 tinha um vídeo explicando tudo isso, tá...
1:07:51 então aí eu explicava isso aqui no
1:07:54 vídeo... e na parte seguinte tem as contas,
1:07:57 que são exatamente essa tradução das
1:07:58 contas do Thompson que ele faz
1:08:01 alternando português e notação
1:08:03 matemática para uma notação toda com
1:08:06 contas um pouquinho mais moderna, com
1:08:08 esse truque de que o "antes" vira
1:08:12 "subscrito 0", o "depois" vira
1:08:12 "subscrito 1",
1:08:15 e a gente vai fazer várias distinções
1:08:17 que ele não faz... por exemplo vai ter um
1:08:19 determinado lugar em que ao invés de
1:08:21 dizer "igual" eu uso o sinal de
1:08:22 "aproximadamente".

1:08:29 Eu acabei não criando links pra
1:08:32 discussão correspondente, que virou um
1:08:35 super exercício que a gente fez em sala
1:08:37 em Cálculo 3, que era tentar entender
1:08:42 dois exemplos do livro do Daniel Miranda
1:08:45 sobre
1:08:47 quantidades que variam juntas... peraí,
1:08:50 deixa eu só lembrar qual é exatamente
1:08:53 o termo para isso... desculpa, minha memória
1:08:55 é péssima, tem um termo padrão para isso...
1:09:05 "taxas de variação".

1:09:10 Bom, então repara, eu tava tentando
1:09:13 preparar os alunos para entenderem
1:09:15 taxas de variação, entenderem
1:09:18 infinitesimais, entenderem como
1:09:20 linearizar coisas... e como muitos alunos
1:09:23 não estavam entendendo esse tipo de
1:09:26 exercício daqui...
1:09:28 peraí, deixa eu ver se eu consigo
1:09:30 encontrar... é o exercício do Thomas.

1:09:35 Aqui. Os livros fazem muitas
1:09:39 figuras desse tipo, principalmente em
1:09:41 Cálculo 3, que são superfícies que são
1:09:43 dadas por
1:09:45 fórmulas simples, mas eles não mostram
1:09:48 qual é a fórmula...

1:09:51 Lembrem que quando eu falei um pouquinho
1:09:53 da minha apresentação... peraí, deixa eu
1:09:55 fechar um monte de janelas aqui...
1:10:04 lembra que na minha apresentação sobre
1:10:06 aulas por Telegram eu falei de uma coisa
1:10:09 que eu tentei trabalhar com os alunos...
1:10:11 é o seguinte.

1:10:22 Eu tentei trabalhar com os alunos essa idéia
1:10:24 de que toda vez que o livro faz uma
1:10:26 figura pro caso geral na verdade essa
1:10:29 figura é uma figura pra um caso
1:10:30 particular na qual vários números foram
1:10:33 apagados... então
1:10:36 no caso particular esse alfa é 3/2,
1:10:39 esse beta é 2, e todos os pontos
1:10:43 têm coordenadas simples, mas no caso
1:10:45 geral a gente não vê mais número nenhum...

1:10:48 aí a gente tem que imaginar que essa
1:10:50 figura daqui é algo no qual alfa é um
1:10:52 número qualquer, beta é um número
1:10:54 qualquer, P é um ponto qualquer, etc,
1:10:56 u e v são vetores quaisquer,
1:10:59 e coisas assim...

1:11:02 E aí tem uma idéia que eu trabalhei
1:11:04 muito no nos meus cursos mas que ela
1:11:07 ainda não tinha um slogan...
1:11:11 e o slogan atualmente é "vire seu próprio
1:11:15 GeoGebra". Deixa eu explicar o que que é
1:11:18 isso. Todos os alunos que chegam nas
1:11:20 minhas matérias eles já viram um pouquinho
1:11:21 de GeoGebra nas matérias anteriores...
1:11:24 quase ninguém aprendeu a usar GeoGebra
1:11:27 mas as pessoas viram os professores
1:11:28 usando isso nas aulas e nas
1:11:30 apresentações,
1:11:32 e no GeoGebra você tem figuras como essa
1:11:36 daqui, em que você tem sliders como esses
1:11:40 e mudando os sliders você consegue mudar
1:11:43 determinados parâmetros e a figura muda...

1:11:45 nesse exemplo
1:11:49 esse terceiro slider controla o
1:11:52 raio do círculo e esses dois primeiros
1:11:55 sliders controlam a coordenadas x e a
1:11:57 coordenada y do
1:11:59 centro do círculo.

1:12:02 Então, um dos objetivos dos meus cursos
1:12:04 era preparar os alunos para eles
1:12:08 conseguirem visualizar essas coisas que
1:12:10 o Geogebra faz mentalmente...

1:12:13 E tinha um montão de exercícios pra isso.
1:12:16 Em alguns exercícios eles tinham que se
1:12:19 juntar em grupos, apontar coisas, fazer
1:12:21 mímicas e não sei que, e nesses exercícios
1:12:24 eles iam acabar aprendendo a fazer
1:12:29 mímicas que os colegas entendessem...

1:12:33 Lembra que lá atrás eu falei de
1:12:35 exercícios de apontar pra retas em R^3
1:12:38 com a ponta de uma caneta...
1:12:41 e quando as aulas eram presenciais antes
1:12:44 da pandemia eles faziam isso com
1:12:46 modelinhos de papel e arame, e dava super
1:12:48 certo.

1:12:53 Outra coisa que eu tentei fazer para
1:12:54 tentar fazer os alunos se acostumarem
1:12:56 com essa idéia de que eles vão ter que
1:12:58 virar o próprio GeoGebra é o seguinte.
1:13:01 Teve uma aula de cálculo 3 no qual a
1:13:03 gente trabalhou um determinado vídeo...
1:13:06 na verdade
1:13:08 quatro minutos e meio de um determinado
1:13:10 vídeo maravilhoso que é uma introdução
1:13:12 a splines feito pela Freya Holmér...
1:13:16 e aí eu aqui botava a legenda da parte
1:13:20 importante do vídeo,
1:13:22 e aqui tinha três fotogramas do vídeo,
1:13:28 e a parte mais importante do vídeo...
1:13:31 Deixa eu ver se eu consigo reduzir o
1:13:33 volume aqui, que
1:13:35 o som do computador tá horrível...

1:13:39 Então nesse trecho a gente tinha essa
1:13:41 figura na qual o tempo variava e aí
1:13:44 várias quantidades variavam junto com o
1:13:45 tempo, aí o comprimento desses vetores
1:13:47 variava junto, e aí ela mudava o modo
1:13:51 de somar esses vetores, e aparecia
1:13:53 uma spline.

1:13:56 E era legal porque os alunos ficavam
1:13:58 empolgadíssimos com isso. Eles já viram
1:14:00 coisas parecidas, mas eles ainda não
1:14:03 tinham estrutura mental pra conseguir
1:14:04 visualizar essas coisas eles mesmos, e eu
1:14:07 comecei a tentar produzir exercícios
1:14:11 para eles treinarem isso.

1:14:14 E lembrem que lá atrás eu disse que meus
1:14:17 exercícios às vezes não funcionavam, e
1:14:19 eu ia melhorando eles de um semestre pro
1:14:21 outro...

1:14:24 Eu tentei fazer vários exercícios de
1:14:27 desenhar trajetórias,
1:14:29 e eles começavam desenhando trajetórias
1:14:31 que davam círculos, depois umas trajetórias
1:14:32 que davam parábolas...
1:14:34 aliás, desculpa, começavam
1:14:37 corm retas, que eram simplíssimas, depois
1:14:39 círculos, parábolas, e coisas assim, e aí
1:14:42 no último semestre eu fiz um exercício
1:14:45 que foi muito legal, que era o seguinte...

1:14:50 Depois deles terem treinado essas
1:14:52 trajetórias mais simples eu dava uma
1:14:55 definição de uma trajetória cujo
1:14:58 resultado ia ser isso - ia ser uma curva
1:15:01 dessas em que o nosso ponto faz isso
1:15:03 aqui...

1:15:08 E aí nesse ponto eles já tinham aprendido
1:15:11 a calcular o vetor velocidade de uma
1:15:13 trajetória e algumas outras coisas, e o
1:15:16 exercício desse dia era um exercício em
1:15:18 grupo no qual eu dizia: agora vocês vão
1:15:22 se juntar e vão tentar fazer uma
1:15:23 aproximação pro desenho dessa curva
1:15:26 daqui,
1:15:27 mas vocês não podem escrever nenhuma
1:15:30 letra e nenhum número.

1:15:32 E aí eu dava alguns truques, eles
1:15:35 começavam a ver como como pegar um vetor
1:15:37 e multiplicar ele por dois ou dividir
1:15:40 ele por 2, como fazer várias coisas no
1:15:41 olho, como pensar em termos de 30 graus,
1:15:44 60 graus e coisas assim, e aos pouquinhos
1:15:48 isso ia funcionando... alguns alunos
1:15:50 ficaram empolgadaços, mas óbvio
1:15:53 que outros alunos empacavam, né... mas
1:15:55 funcionou bastante bem.

1:15:57 E no final eu mostrava o gabarito
1:16:00 mostrando que
1:16:01 a curva feita pelo computador era
1:16:04 exatamente isso, e muita gente tinha
1:16:06 chegado a algo muito próximo disso.

1:16:10 E repara que tem vários truques
1:16:13 aqui feitos pros alunos não poderem
1:16:15 fazer as contas...
1:16:17 tem ângulos de 30 e 60 graus, então se os
1:16:21 alunos forem tentar
1:16:22 fazer contas usando raízes quadradas eles
1:16:25 vai levar um tempão... então eu ia dando
1:16:27 dicas para eles fazerem aproximações...

1:16:34 Tinha uma outra coisa que eu queria que
1:16:36 os alunos aprendessem a visualizar. Eu
1:16:38 mostrava animações disso e depois a
1:16:40 gente passava várias aulas trabalhando,
1:16:41 porque se eles aprendesse, a visualizar
1:16:44 isso eles mesmos
1:16:47 vários conceitos de Cálculo 2
1:16:49 ficavam fáceis... por exemplo o conceito
1:16:52 de funções não integráveis, que são
1:16:54 não integráveis porque a aproximação
1:16:56 por retângulos por cima dá um resultado
1:16:58 diferente da aproximação por retângulos
1:17:01 por baixo...

1:17:03 E aí uma das animações que eu fiz foi
1:17:05 essa... não é uma animação de verdade, mas é
1:17:07 um PDF em que se eu apertar PgUp e PgDn várias
1:17:11 vezes a gente passa para vários
1:17:13 fotogramas...
1:17:14 em que no início
1:17:16 o meu intervalo original, que é de 0 até 7,
1:17:20 tá dividido em 4 subintervalos, depois
1:17:23 ele passa a ser dividido em 8, e depois
1:17:25 em 16, depois em 32, depois em 64,
1:17:30 depois em 128... e a gente tinha vários
1:17:33 exercícios pros alunos irem aprendendo a
1:17:36 fazer essas
1:17:39 aproximações aqui sem contas...
1:17:42 e alguns alunos empacavam muito nisso.

1:17:45 Deixa eu mostrar uma outra coisa na qual
1:17:48 os alunos tiveram muita dificuldade, e eu
1:17:50 levei MUITO tempo para encontrar o
1:17:53 exercício que funcionava bem e rápido.
1:17:57 É o seguinte...

1:18:01 A "nossa função preferida" é uma parábola.
1:18:03 Eu não tô num programa que seja fácil de
1:18:06 desenhar ela então eu vou só fazer a
1:18:07 mímica dela, tá. Ela faz assim... aqui ela
1:18:11 passa pelo ponto (0,0), pelo ponto (4,0),
1:18:13 e aqui no meio ela tem altura 4.

1:18:18 E aí tem exercícios de desenhar essa
1:18:20 parábola, e nesse processo os alunos vão
1:18:24 ter que reaprender o significado visual
1:18:26 da derivada e coisas assim.

1:18:30 E aí depois disso eu começava a dar
1:18:33 exercícios de representar pontos dessa
1:18:35 forma daqui.
1:18:37 E tinha vários alunos que tinham muita
1:18:40 dificuldades para entender que você pode
1:18:42 encontrar esse ponto daqui encontrando x
1:18:44 e depois subindo o ponto com coordenadas
1:18:48 (x,0) até a curva...

1:18:50 Aí a primeira coisa que eu consegui que
1:18:52 me ajudou um pouquinho foi chamar os
1:18:54 dois modos de encontrar esse ponto de
1:18:56 "jeito burro" e "jeito esperto"...

1:18:58 do "jeito burro" você
1:19:00 calcula f(x), e em alguns casos as
1:19:04 contas são trabalhosas... por exemplo
1:19:05 quando x=2.5, f(2.5) vai dar 3.75, mas
1:19:11 eu só consigo fazer isso com todos esses
1:19:14 passos daqui... e aí se você for usar o
1:19:17 jeito burro você primeiro encontra
1:19:20 y=3.75 no eixo y,
1:19:23 e aí esse ponto praticamente nunca vai
1:19:27 cair em cima da sua parábola...
1:19:30 nossos desenhos são meio tortos e esse
1:19:32 ponto acaba caindo em outro lugar.

1:19:35 E o "jeito esperto" é você encontrar no
1:19:37 eixo x esse ponto daqui, aí depois você
1:19:40 sobe ele pra curva, e aí, olha lá!
1:19:43 Você encontrou o ponto (2.5,f(2.5))!
1:19:47 Muitos alunos tinham uma dificuldade
1:19:48 inacreditável com isso.
1:19:51 Eu cheguei a fazer vários vídeos sobre
1:19:54 isso, e a cada vez eu ia encontrando
1:19:56 um jeito um pouquinho melhor
1:19:58 de apresentar isso em vídeo...

1:20:03 E aí teve um determinado momento em que
1:20:06 encontrei um exercício maravilhoso pra
1:20:08 isso.

1:20:10 Bom, primeiro teve um slogan que era
1:20:14 "um dos nossos objetivos é aprender
1:20:16 a NÃO CALCULAR"...

1:20:18 aqui tem um dos vídeos em que eu
1:20:21 mostrava como subir o ponto para curva...
1:20:23 eu abaixei o volume do computador
1:20:25 bastante porque o som do computador tá
1:20:28 horrível...
1:20:33 ah, deixa eu aumentar a velocidade muito.

1:20:38 Então eu apresentava isso em vídeo,
1:20:45 depois eu comecei a aplicar vários slogans,
1:20:53 comecei a dizer coisas tipo: se você não
1:20:55 aprender a usar o jeito esperto você vai
1:20:57 demorar muito, seu retângulo - porque a
1:21:00 gente queria interpretar determinados
1:21:02 coisas como somas de retângulos, então
1:21:06 a gente interpretava isso aqui como um
1:21:08 retângulo, isso aqui como a altura do
1:21:10 retângulo e isso aqui como a base do
1:21:11 retângulo...

1:21:12 se você não aprender a usar o jeito esperto
1:21:14 você vai demorar muito, o seu retângulo
1:21:16 não vai ter um vértice sobre a parábola
1:21:18 e você nunca vai virar o Bob!
1:21:20 O objetivo é virar o Bob, que
1:21:22 consegue fazer essas coisas rápido e com
1:21:24 super pouca conta, porque ele sabe os
1:21:27 truques para visualizar as coisas e
1:21:29 fazer muita coisa visualmente ao invés
1:21:31 de fazer tudo por conta.

1:21:34 Então isso aqui foi a minha versão de
1:21:36 2020.2.
1:21:39 Deixa eu mostrar uma versão muito mais
1:21:42 recente disso.
1:21:46 O enunciado é o mesmo,
1:21:49 só que eu fiz essas figuras aqui. Eu
1:21:53 imprimia elas na papelaria, eu
1:21:56 trazia um montão de cópias pros
1:21:57 alunos, e eu pedia pros os alunos
1:21:59 representarem todos esses somatórios
1:22:01 nessas figuras.

1:22:02 E aí eles não tinham mais como calcular
1:22:04 o que que era f(x)... não tem conta para
1:22:07 fazer, eles tinham que fazer tudo visualmente!
1:22:10 Então o único modo de você calcular o
1:22:12 que que é f(x2) nesse gráfico daqui é você
1:22:15 pegar esse ponto x2 daqui, subir ele até
1:22:18 aqui, e interpretar que o f(x2) é a altura
1:22:21 desse ponto.

1:22:24 E... caramba, eu levei vários semestres
1:22:27 para chegar nesse exercício daqui!

1:22:32 Então, voltando...
1:22:35 tem um monte de exercícios que vale
1:22:38 muito a pena compartilhar. E se eu
1:22:40 já tivesse acesso aos exercícios que
1:22:43 outras pessoas fizeram eu estaria
1:22:45 economizando um tempo gigantesco.

1:22:48 Lembra que o Henrique Sá Earp tava tentando
1:22:50 organizar um modo das pessoas trocarem
1:22:53 material dos seus cursos...

1:22:55 tem um momento na
1:22:58 apresentação sobre aulas por Telegram em
1:23:01 que ele disse: "Eduardo, deixa eu contar
1:23:03 uma coisa? Eu tô fazendo esse esquema
1:23:05 aqui do Google Drive, não sei quê..."
1:23:07 E ele comenta que se a gente conseguir usar
1:23:09 provas uns dos outros a gente já vai ter
1:23:11 um ganho de escala enorme
1:23:14 por exemplo eu posso usar uma prova que
1:23:16 o Fulano de Tal fez, que é uma prova
1:23:19 ótima, em que o Fulano caprichou muito
1:23:22 naquela prova, e que é uma prova que vai ser
1:23:24 totalmente nova para mim e pros meus
1:23:25 alunos...

1:23:27 E aí se a gente puder fazer isso
1:23:30 o tempo que a gente gastaria preparando
1:23:33 aquela prova a gente pode gastar
1:23:35 melhorando outra parte do curso... e aí ele
1:23:38 usa a expressão "ganho de escala" - isso
1:23:40 nos dá um ganho de escala incrível.

1:23:43 E aí ele fala em usar aulas de outras
1:23:45 pessoas, usar provas de outras pessoas,
1:23:47 e o que eu tou querendo falar nesse vídeo
1:23:50 é que existem outras coisas muito úteis
1:23:52 que valem muito a pena compartilhar e que
1:23:55 são menos óbvias... e eu tô chamando elas
1:23:58 de "slogans". Tem vários slides que eu
1:24:00 tou usando aqui sobre mudar
1:24:02 o modo de pensar, aprender modos novos
1:24:04 de estudar, modos novos de fazer
1:24:07 exercícios, e tal, que não são nada óbvios.
1:24:09 Às vezes os alunos estão acostumados
1:24:11 com um determinado modo e dá um
1:24:13 trabalhão para gente mostrar que: olha,
1:24:16 nessa matéria vai ser melhor você usar
1:24:18 um modo completamente diferente...

1:24:21 Deixa eu dar um exemplo que eu acho que
1:24:23 aqui eu pulei... é, pulei sim, caramba!
1:24:35 Uma dessas coisas,
1:24:38 que também não foi nada óbvia para mim
1:24:40 quando eu descobri, que é o seguinte...
1:24:43 tem um momento em Cálculo 2 em que a
1:24:46 gente estava lidando com partições, então
1:24:48 a gente tinha que pegar um determinado
1:24:50 intervalo e partir ele em, digamos oito
1:24:53 pedaços iguais, e aí os alunos achavam
1:24:57 que eles tinham que simplificar a
1:25:00 coordenada x desse intervalo, então eles
1:25:02 achavam que eles tinham que escrever os
1:25:05 pontos dessa partição desse jeito daqui:
1:25:08 0, 1/4, 1/2, 3/4, 1, 5/4, 3/2...
1:25:15 E aí eu mostrava para eles que o melhor
1:25:17 modo de simplificar expressões
1:25:21 depende do contexto, e se nesse caso a
1:25:24 gente escrever os pontos da partição
1:25:25 desse jeito fica muito mais fácil
1:25:27 entender que pontos são esses.

1:25:30 E aí eu também fui produzindo várias
1:25:32 versões disso,
1:25:34 e eu acho que eu tenho aqui um link pra
1:25:37 uma versão muito antiga disso...
1:25:41 aqui ó: é um ponto do log
1:25:44 das aulas por Telegram
1:25:48 em que eu digo pro João: olha, se você
1:25:53 fizer isso vai dar umas expressões que
1:25:55 se você simplificar elas e transformar
1:25:57 elas em números ninguém vai entender...
1:25:59 aí o João pergunta: ok, então eu paro nas
1:26:01 expressões? E eu digo: sim! E eu tinha até
1:26:05 escrito uma outra frase antes
1:26:06 disso, que é: por exemplo, eu não conheço
1:26:09 ninguém que eu olhe para -0.7568024...
1:26:11 e pense: "opa, isso é sen(4)!"...

1:26:26 Teve uma outra coisa que eu achei super
1:26:28 útil, que foi o seguinte...
1:26:30 os alunos começaram a querer saber qual
1:26:33 era a definição certa de "simplificar".
1:26:35 E aí eu tive que mostrar o seguinte... eu
1:26:39 disse: isso é um daqueles assuntos que é
1:26:41 muito mais difícil do que parece...
1:26:44 um bom lugar pra gente descobrir que
1:26:48 "simplificar" é composto de várias
1:26:50 operações diferentes
1:26:52 e cada uma delas tem um nome
1:26:55 é a documentação dos programas
1:26:58 de computação simbólica.

1:27:00 Então, por exemplo, a gente pode olhar
1:27:02 para esse livro daqui, que é um livro
1:27:06 sobre Maxima...
1:27:09 ele tem um capítulo inteiro sobre
1:27:11 simplificação e ele
1:27:14 descreve alguns tipos de
1:27:16 simplificação que você pode
1:27:19 ligar ou desligar, ativar ou desativar, e
1:27:23 se você configura esses tipos de
1:27:25 simplificação a noção do Maxima do que
1:27:28 que é simplificar uma expressão muda...
1:27:32 e cada tipo de simplificação desses
1:27:34 também corresponde a uma função que vai
1:27:36 pegar uma expressão original e vai
1:27:38 tentar transformar elas de uma
1:27:39 determinada forma fazendo só aquela
1:27:41 simplificação.

1:27:44 E aí eu também mostrava isso no manual
1:27:48 do Maxima. Tem uma página do manual do
1:27:51 Maxima que se chama "Introduction
1:27:53 to Simplification",
1:27:55 que já é meio grandinha...
1:27:58 e aí depois tem uma outra página enorme,
1:28:04 que é tudo isso aqui,
1:28:07 que descreve várias funções e
1:28:11 vários flags que controlam a
1:28:14 simplificação. E aí quando eu mostrava
1:28:16 isso os alunos ficavam super felizes, era
1:28:18 uma resposta honesta que mostrava pra
1:28:20 eles onde tem os detalhes, e eles se
1:28:22 convenciam de que provavelmente não vale
1:28:25 a pena entender esses detalhes agora, mas
1:28:27 se eles tiverem curiosidade eles podem
1:28:29 olhar para isso depois.

1:28:31 Então tem muita coisa nos meus cursos
1:28:34 que fica muito mais fácil explicar,
1:28:36 responder, etc, se eu consigo apontar
1:28:39 para onde tem os detalhes daquilo.
1:28:43 Deixa eu ver aqui que eu quero mostrar
1:28:45 agora... pera aí... já sei. Eu quero
1:28:55 mostrar mais alguns slogans, tá...

1:29:07 É o seguinte.
1:29:19 Primeiro: durante a pandemia
1:29:23 o meu modo de lidar com perguntas era
1:29:26 muito mais simples
1:29:28 e eu repetia várias vezes durante as
1:29:31 aulas coisas tipo isso aqui...

1:29:39 eu dizia que todas as perguntas eram
1:29:41 bem-vindas,
1:29:43 e aí tem esse trecho, que deixa eu ler
1:29:46 pra vocês... eu respondi isso aqui
1:29:48 pra alguém:

1:29:50 Lembra também que todas as vezes que alguém
1:29:52 me perguntou algo - mesmo que fosse algo de
1:29:54 matéria bem antiga, ou de outro curso ou
1:29:56 algo que podia parecer uma
1:29:58 pergunta burra -
1:30:00 imediatamente aquela pessoa virou a
1:30:01 melhor pessoa do mundo para mim e eu
1:30:03 tratei a pessoa super bem...
1:30:06 Mas é como eu expliquei no vídeo, cada
1:30:08 exercício de uma página tem centenas
1:30:10 de idéias por baixo, não sei quê...
1:30:12 então não basta vocês
1:30:14 dizerem "professor, faz um vídeo", ou
1:30:16 "professor, explica o exercício tal"...
1:30:18 cada
1:30:19 coisa dessas tem centenas de sub-idéias e
1:30:22 para mim é muito melhor que eles façam
1:30:24 perguntas bem mais
1:30:25 específicas para eu saber o que que eu
1:30:27 tenho que detalhar.

1:30:28 E aí eu tenho a impressão de que no outro
1:30:31 vídeo eu falei de um vídeo que é
1:30:33 especificamente sobre isso...
1:30:36 siim, falei! Deixa eu mostrar ele aqui, ó...
1:30:42 Aqui tá a página das reclamações sobre o
1:30:45 CAEPRO...
1:30:50 E aí aqui tem alguns vídeos antigos, e um
1:30:54 dos vídeos antigos é esse:
1:30:56 Dicas de estudo pro "integrais como
1:30:58 somas de retângulos (1)".

1:31:05 E aí tem as legendas aqui, e deixa só
1:31:08 reler um pedacinho daqui...

1:31:13 na aula passada várias pessoas disseram
1:31:15 que não estão entendendo nada e que os
1:31:16 vídeos que eu fiz não estão ajudando
1:31:17 nada...
1:31:19 e eu passei um tempo sem saber como
1:31:20 responder, né, porque em Matemática é
1:31:22 assim o tempo todo, e não sei quê não
1:31:24 sei quê...

1:31:29 E aí blablá... então eu resolvi interpretar o
1:31:32 que as pessoas estavam dizendo como: eu
1:31:34 não tô entendendo nada e eu não sei como
1:31:36 estudar, e eu não sei como
1:31:38 sair desse ponto, eu não sei como começar
1:31:41 a entender aos pouquinhos até conseguir
1:31:44 entender tudo.

1:31:46 E aí eu preparei esse vídeo, que é sobre
1:31:49 algumas das técnicas de
1:31:52 decompor dúvidas muito grandes em um
1:31:55 montão de dúvidas menores.

1:31:58 Voltando.
1:32:14 Então, aqui tem vários trechinhos sobre
1:32:16 como é que eu tava lidando com perguntas...
1:32:19 vários dessas são coisas que eu já falei...

1:32:21 tinha algumas sutilezas,
1:32:24 nem sempre toda pergunta é bem-vinda,
1:32:27 tinha algumas perguntas que eu
1:32:29 dizia algo tipo: essa pergunta eu não
1:32:32 posso responder porque se eu fizer eu
1:32:33 vou estar fazendo o papel do colega que
1:32:35 é muito seu amigo
1:32:37 e você vai achar que pode fazer isso na
1:32:39 prova...

1:32:42 tem um momento aqui
1:32:45 em que alguém me pergunta algo sobre
1:32:47 métodos
1:32:49 e eu respondo isso aqui: eu prefiro não
1:32:53 responder perguntas sobre métodos porque
1:32:55 às vezes ou eu entendo a pergunta errado
1:32:57 ou a pessoa entende a minha resposta
1:32:59 errado e aí ela faz algo
1:33:03 errado na prova e fica p* da vida
1:33:04 comigo, mas se você me mandar exemplos
1:33:07 eu checo tudo em detalhes!

1:33:09 Então a idéia é:
1:33:11 se a pessoa me perguntar algo sobre um
1:33:13 método eu digo "me dá um exemplo e vamos
1:33:16 discutir o exemplo".

1:33:23 Deixa eu ver...
1:33:26 tem um outro lugar em que eu
1:33:28 respondo a mesma coisa
1:33:31 isso aqui também sobre essa história de
1:33:34 eu fazer o papel do colega que é muito
1:33:35 seu amigo...

1:33:36 e digo que algumas
1:33:42 questões vão precisar ter os trechos em
1:33:45 português, e o colega que seja muito
1:33:48 amigo de vocês pode até aceitar uma
1:33:49 solução que não tem os trechos em
1:33:51 português, mas se eu aceitar minha vida
1:33:52 vira um inferno...

1:33:58 Deixa eu aproveitar e mostrar uma
1:34:00 situação na qual tive que exigir que as
1:34:01 pessoas colocassem os trechos em
1:34:03 português na prova. É o seguinte. No
1:34:06 último semestre
1:34:08 na P2 de Calculo 2 eu pedi para as
1:34:12 pessoas resolverem uma determinada EDO
1:34:14 e encontrarem
1:34:15 duas soluções diferentes para essa EDO,
1:34:18 com condições iniciais diferentes...

1:34:22 E aí na VS eu disse o seguinte...
1:34:30 deixa eu ler isso aqui...
1:34:36 eu lembrava aqui o que a gente tinha visto
1:34:38 no curso... o primeiro exemplo de uma
1:34:41 EDO com variável separáveis que a gente viu
1:34:42 tinha soluções que eram semicírculos
1:34:44 tanto acima do eixo x quanto abaixo
1:34:46 do eixo x...
1:34:50 E aí eu disse isso aqui. Na P2 eu pus uma
1:34:52 questão sobre EDOs com variáveis separáveis
1:34:55 um pouco mais complicada do que essa dos
1:34:56 semicírculos, e
1:34:57 muitas pessoas fizeram erros de conta
1:34:59 horríveis que eu acho que foram causados
1:35:02 por desorganização na hora de fazer
1:35:04 contas... por exemplo, várias pessoas
1:35:06 escreveram H(x)=sqrt(x) num lugar
1:35:09 das contas e H(x)=sqrt(x+3)
1:35:12 em outro...

1:35:15 e aí eu explico que isso casou confusões
1:35:17 e não sei quê, e aí no resto da questão eu
1:35:20 digo...
1:35:22 bom, eu peço para as pessoas resolverem
1:35:23 uma coisa específica com duas soluções
1:35:25 gerais dessa EDO e
1:35:29 depois duas soluções particulares, e eu
1:35:33 digo isso aqui nessa questão: eu vou
1:35:35 avaliar principalmente se você sabe usar
1:35:37 direitos os truques do anexo da página 4.
1:35:40 Ou seja: não basta usar o método.

1:35:43 E os truques do anexo da página 4 são
1:35:46 seguintes. Eu anexei o gabarito
1:35:50 dessa questão da P2, e o gabarito tem
1:35:54 vários dessas partículas em
1:35:56 português... por exemplo, tem
1:36:02 "seja", "temos", "isto é",
1:36:04 "então"... deixa eu encontrar uns
1:36:07 "isto é"s e "então"s... aqui tem
1:36:10 um "isto é"s, aqui tem um "então",
1:36:12 aqui tem um "se"...
1:36:16 Então eu dava isso aqui como referência
1:36:18 e as pessoas que já tinham uma certa
1:36:21 noção de como usar isso conseguiam usar
1:36:23 essa referência desse anexo daqui e
1:36:26 conseguiam escrever bastante bem a
1:36:30 solução delas dessa questão
1:36:32 sem se enrolar...

1:36:39 Deixa eu ver...
1:36:43 eu acho que vale a pena mostrar isso
1:36:45 aqui também...
1:36:47 Siiiim! Peraí, deixa eu mostrar isso aqui
1:36:51 direito.
1:36:56 Quase todas as expressões matemáticas
1:36:58 que a gente usa em Cálculo 2 dependem
1:37:00 do contexto. Por exemplo, a interpretação
1:37:02 default pra essa expressão daqui é a
1:37:04 seguinte: pra toda função f:R->R e pra
1:37:07 todo x pertencente a R temos não sei quê...
1:37:11 então se você só escreve isso aqui e mostra
1:37:14 isso aqui pro colega que seja muito seu
1:37:18 amigo ele vai levar meia hora tentando
1:37:19 adivinhar o qual o contexto e vai
1:37:22 adivinhar. E se ele descobrir em menos de,
1:37:25 digamos, 50 tentativas, ele vai dizer: ok
1:37:28 jóia, tá certo.

1:37:30 Mas o colega que seja menos seu amigo
1:37:32 vai fazer menos tentativas, e
1:37:37 vai ter outros personagens, tipo o monitor,
1:37:40 ou o professor, ou o colega que vai fazer o
1:37:44 papel de advogado do diabo, que vai olhar
1:37:47 uma coisa dessas daqui, que é ambígua, e
1:37:51 vai interpretar de propósito do pior
1:37:53 jeito possível.

1:37:55 E eu coloquei esse comentário aqui, ó:
1:37:57 lembre que quase todo mundo pára de ler
1:38:01 um texto matemático quando vê uma
1:38:02 besteira muito grande escrita nele.

1:38:05 Imagina que um colega que seja menos seu
1:38:07 amigo te mostra a solução dele pra
1:38:09 um problema e te pergunta se ela tá certa.
1:38:11 E a solução dele começa com: "Sabemos que
1:38:14 2=3, então blábláblá". O que você faria?

1:38:19 Se o colega não é muito seu amigo você
1:38:22 pararia imediatamente, né, você nem leria
1:38:24 o resto, você diria que tá tudo errado...
1:38:26 claro que isso é um caso muito extremo
1:38:30 de erro grotesco,
1:38:32 mas a gente quer discutir também os
1:38:35 casos mais sutis em que uma pessoa tá
1:38:38 afirmando uma coisa que tá errada.

1:38:42 E tem um outro lugar...
1:38:46 eu não sei onde é que tá o link para ele,
1:38:48 mas tem um outro lugar em que eu uso
1:38:50 essa idéia, e digo:
1:38:54 nesse ponto daqui se você quiser deixar
1:38:56 tudo totalmente preciso você vai gastar
1:38:58 horas, ou dias... então nesse ponto aqui
1:39:01 escreva como se você estiver escrevendo
1:39:03 para um colega que seja muito seu amigo.

1:39:11 Deixa eu ver, peraí.
1:39:33 Tem uma coisa aqui que o...
1:39:38 Deixa eu falar ela rapidinho porque
1:39:40 isso que eu vou falar agora
1:39:42 vai ser uma espécie de trailer pro
1:39:44 próximo vídeo, tá.

1:39:46 Deixa eu voltar para aquela história da
1:39:48 dica 7. Na dica 7 tem essa idéia de que
1:39:56 você quer virar essa pessoa daqui -

1:40:00 a pessoa que quando as outras pessoas
1:40:01 lêem a sua solução e acham que ela tá
1:40:04 claríssima, e que elas devem estudar
1:40:07 com você...
1:40:09 Você quer virar a pessoa que toda vez
1:40:12 que as pessoas lêem algo que você
1:40:14 escreveu as pessoas ficam maravilhadas e
1:40:16 pensam: UAU, eu quero estudar com essa
1:40:17 pessoa daqui.

1:40:22 Vamos lembrar daquele personagem lá do
1:40:25 início, que era o garoto gênio que
1:40:29 via qualquer problema e dizia: EU SEI,
1:40:31 EU SEI, EU SEI, e aí ele usa um método maluco,
1:40:34 chega numa solução completamente
1:40:35 maluca, e ele tem certeza absoluta daquilo.

1:40:41 Ele não é uma pessoa com quem as outras
1:40:43 pessoas vão querer estudar. Então a
1:40:46 estratégia dele pode funcionar bem a
1:40:47 curtíssimo prazo, porque aí as pessoas
1:40:50 vão achar que...
1:40:53 a curto prazo as pessoas vão achar que
1:40:56 ele é um gênio e vão respeitar ele muito,
1:40:57 mas depois esse respeito vai...
1:41:00 vai até virar do avesso, né, as pessoas vão
1:41:03 pensar "ai meu Deus, aquele cara ele se
1:41:05 acha fodão mas ele é um idiota"...

1:41:09 Uma das idéias dessa dica 7 é a seguinte.
1:41:12 Se você for treinando com os colegas
1:41:15 virar uma pessoa com quem vale a pena
1:41:16 estudar você vai descobrir quais
1:41:20 atitudes funcionam melhor a longo prazo...
1:41:27 e deixa eu mostrar uma coisa aqui...
1:41:33 lembre que isso aqui é aquele meu PDF com
1:41:36 as várias reclamações dos alunos
1:41:37 coloridas de vários jeitos,
1:41:40 e aí no final
1:41:45 várias coisas viraram branco...
1:41:50 e
1:41:58 aí tem vários alunos que não entenderam
1:42:01 a metodologia, não entenderam porque que
1:42:03 eles deveriam estar discutindo uns com
1:42:04 os outros,
1:42:07 e aí tem alguns alunos que... cadê?
1:42:14 Tem alguns alunos que reclamam que
1:42:18 que eu dava... cadê, caramba? Sumiu...
1:42:23 mas bom, eu tenho certeza absoluta de que
1:42:25 tinha alunos dizendo que tentavam
1:42:28 estudar por outros livros e não
1:42:31 funcionava
1:42:32 porque eu tava apresentando a matéria de
1:42:34 um jeito completamente maluco, tá...
1:42:36 diferente dos outros professores,
1:42:38 diferente dos livros, e não sei que.

1:42:41 Lembra que lá no início eu disse que
1:42:43 existem vários modos de estudar pelo
1:42:45 livro.
1:42:47 O que aconteceu no último semestre
1:42:49 é que teve
1:42:52 alguns alunos que começaram a estudar
1:42:55 por outros livros e me mostraram os
1:42:57 livros que estavam estudando.
1:42:59 E eu fiquei empolgadíssimo com isso, e aí
1:43:03 eu mostrei pra eles por que que eu tava
1:43:04 apresentando as coisas de uma determinada
1:43:06 forma, e mostrei que o que o que os
1:43:08 outros livros estavam fazendo era algo
1:43:10 avançado
1:43:11 que eu achava difícil que eles
1:43:13 conseguissem aprender direto aquilo. Então
1:43:15 no meu método a gente estava dividindo a
1:43:18 habilidade que
1:43:20 o livro queria que você desenvolvesse
1:43:24 em várias habilidades diferentes para eles
1:43:25 poderiam aprender um passinho de cada vez,
1:43:27 e eles adoraram isso. Alguns alunos me
1:43:30 mostraram outros livros, e alguns alunos
1:43:33 não.

1:43:37 Então,
1:43:39 parece que tinha uns alunos que estavam
1:43:42 tentando estudar por outro lugar, mas
1:43:43 eles não me contaram que que era esse
1:43:45 outro lugar... e repara, eu tava tentando
1:43:47 criar uma rede de pessoas que
1:43:49 compartilhavam material, e toda vez que
1:43:51 eu vi material de outras pessoas era
1:43:53 muito legal, eu sempre aprendi alguma
1:43:55 coisa nova quando eu olhava o material
1:43:57 de algum outro curso... e eu tinha alunos
1:44:00 que resolveram não me contar
1:44:03 por onde é que ele estava estudando,
1:44:04 não compartilhar esse material comigo, e
1:44:07 depois anda reclamaram...

1:44:12 E aí a sensação que eu tenho é a
1:44:14 seguinte. Essa atitude, de
1:44:19 não entender que o professor tá
1:44:21 pedindo "oi gente, compartilhem o material
1:44:23 de outros lugares comigo" e de não contar
1:44:26 nada pro professor, só fazer
1:44:28 reclamações no final do semestre, essa é
1:44:31 uma atitude que não é boa a longo prazo.

1:44:32 Vamos voltar aqui para dica 7...
1:44:36 Eita, fechei tudo... deixa abrir ela de novo...
1:44:54 então, isso não é bom, é como se eles não
1:44:57 tivessem descoberto que essa estratégia
1:44:59 não é boa, que se seguirem essa
1:45:01 estratégia ninguém vai querer estudar
1:45:02 com eles no futuro...

1:45:06 caramba que mais que eu queria falar?...
1:45:11 Meu Deus, desculpem a bagunça...
1:45:20 droga, digamos que era isso, tá? Eu tinha
1:45:24 material demais, eu não consegui
1:45:25 organizar ele de um modo 100% organizado,
1:45:29 eu não tenho um jeito
1:45:31 maravilhoso de fechar esse vídeo com
1:45:34 chave de ouro, então vou parar o vídeo
1:45:36 por aqui assim mesmo.
1:45:42 É isso!

1:45:44