Cabos na diagonal (Cálculo 3, 2021.2

Mais informações aqui:
Sobre as reclamações do CAEPRO.
Pra assistir o vídeo clique ou no thumbnail abaixo
ou nas marcas de tempo nas legendas.
As legendas dele em Lua estão aqui.

00:00 Oi! Hoje é 17/dez/2021, a data tá aqui
00:03 no cantinho, e
00:06 eu tou fazendo esse vídeo aqui pra
00:09 explicar um detalhe que pode ser
00:10 importante para várias pessoas. A gente
00:11 está trabalhando nesse PDF daqui,
00:13 chamado "Diagramas de numerozinhos",
00:15 e uma das primeiras coisas que ele
00:18 explica é que a gente vai fazer
00:20 diagramas de numerozinhos
00:21 interpretando cada numerozinho como
00:23 a altura de um poste, e a gente vai ligar
00:26 o topo de cada poste aos topos dos
00:29 postes vizinhos usando cabos que são
00:31 segmentos de reta.
00:32 Deixa eu explicar o que isso quer
00:34 dizer. Peraí, deixa eu ver... eu vou
00:39 pegar um outro PDF antigo que a gente tá
00:41 usando nos exercícios, e a gente tá
00:43 tratando os problemas dele que têm figuras
00:45 e gabarito como exercícios. Então tem
00:48 alguns exercícios que a gente tá fazendo
00:49 que têm gabarito com figura e outros que
00:51 não têm, e que vocês vão ter que descobrir
00:53 a cara deles sozinhos.

00:55 Então, a gente tá usando
01:00 exercícios desse PDF aqui, do semestre
01:02 passado...
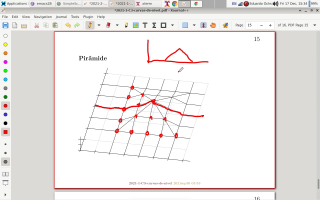
01:04 e dois dos exercícios dão essas figuras
01:09 daqui, ó: um dá uma pirâmide e o outro dá
01:12 uma cruz. Essa pirâmide daqui o diagrama
01:15 de numerozinhos dela é o seguinte...
01:18 aqui tá o eixo x, aqui tá o eixo y...
01:21 o eixo x tá aqui, aqui tá o y...
01:25 aqui tá o eixo z, e
01:29 aqui a altura é 0, 0, 0, 0, 0, 0, 0...
01:36 e aqui começa a pirâmide. Em
01:40 todos esses lugares daqui a altura é 1,
01:47 e aqui no topo da pirâmide a altura é 2.

01:51 Esse zeros a gente pode interpretar como
01:53 querendo dizer que os postes aqui têm altura
01:55 0, aqui também tá cheio de postes de altura 0,
01:57 ó...
01:59 esse 1 quer dizer que tem um poste de altura
02:02 1 aqui, aqui também, aqui também, aqui
02:04 também, etc, e esse 2 quer dizer que
02:08 aqui tem um poste de altura 2. E depois
02:11 a gente liga os postes nos postes vizinhos,
02:13 então por exemplo esse ponto daqui, esse
02:16 poste de altura 0, o topo dele, que tá no chão,
02:18 é ligado nesses quatro outros topos
02:23 daqui... esses três aqui tão no chão e
02:26 esse aqui tá na altura 1.

02:29 E
02:31 em geral se a gente só fizer isso, só
02:34 ligar cada poste nos postes vizinhos a
02:36 gente consegue bastante informação útil...
02:39 e vocês vão ver que muitas vezes os
02:42 programas que fazem gráficos usam essas
02:45 aproximações por quadradinhos - deixa eu
02:46 mostrar uma figura pra vocês...
02:50 cadê? cadê? Ah, aqui.
02:58 Aqui a gente tem uma figura bem maior,
03:02 com um monte de coisa que eu não
03:03 conseguiria calcular na mão, porque tem
03:06 umas exponenciais, talvez tenha uma raiz
03:09 quadrada, sei lá... e isso aqui é um
03:11 diagrama de numerozinhos com os
03:13 postes ligados uns nos outros, e os
03:16 quadrados coloridos de acordo com a
03:19 altura deles... então se eu
03:22 mudar a perspectiva pra cá vocês vão
03:24 ver que todo mundo que tem altura 0...
03:26 aliás, desculpa, altura -10, é preto, depois
03:30 eles vão ficando azuis até esse ponto
03:32 daqui, em que eles ficam vermelhos, e aí
03:35 quando a gente segue para cá, até aqui, a
03:38 gente vê que os quadradinhos que têm
03:41 altura 10 tão amarelos. Então tem um
03:44 espectro de cores aqui, que é um bom modo de
03:46 visualizar a altura de cada coisa, só que
03:49 seria impossível desenhar isso que na mão,
03:50 né, a gente teria que ter, sei lá, uma caixa
03:54 de lápis de cor caríssima que ocuparia uma
03:56 estante inteira e nenhum de nós tem
03:57 dinheiro para isso. Então, reparem que
04:00 que a gente consegue
04:03 ver os quadradinhos aqui, a gente
04:05 consegue ver as curvas que eles fazem...
04:08 por exemplo, aqui a gente vê que a curva
04:11 sobe, depois desce, não sei que... dá pra
04:14 gente ver um bocado de coisa com isso.

04:17 Nos exercícios que a gente tá
04:19 fazendo
04:23 a gente vai ter um problema, que é o
04:25 seguinte...
04:27 se a gente ligar
04:33 esse poste aqui...
04:35 qdz, não, desculpa, dxô falar
04:37 de outro jeito... a gente não sabe
04:39 direito o que que tem no miolo desse
04:41 quadrado, e tem duas escolhas naturais pra
04:45 gente desenhar o que tem aí dentro,
04:47 e elas vão fazer muita diferença...
04:50 então, se eu ligo
04:53 esse poste a esse eu vou ter
04:56 um cabo na diagonal, na diagonal desse
04:59 quadrado daqui, que vai da altura 0 pra
05:01 altura 1, e
05:03 gente consegue ver que no ponto médio
05:05 desse cabo a altura é 0.5.

05:09 mas se eu tivesse escolhido ligar a
05:11 a outra diagonal - ao invés de ligar essa
05:14 diagonal se eu tivesse escolhido ligar essa,
05:17 poste daqui estaria todo no chão...
05:19 ele vai de um poste... desculpa, esse
05:21 cabo estaria todo no chão, ele vai de um
05:23 poste de altura 0 para um outro poste de
05:25 altura 0, e aí o ponto médio desse
05:29 cabo tem altura 0 também, porque
05:31 a média de 0 e 0 é 0...
05:34 então a altura do ponto médio
05:38 dessa diagonal daqui é 1/2 e a altura do
05:41 ponto médio dessa diagonal daqui é 0 -

05:43 uma tá bém mais alta que a outra.
05:47 E isso vai fazer diferença nas
05:50 nossas figuras.
05:52 Eu consegui fazer um desenho do que
05:54 acontece quando a gente faz uma pirâmide
05:56 parecida com essa, só que eu pouco maior,
05:58 e em um dos lugares ao invés da gente
06:00 desenhar o cabo do meio nessa direção -
06:02 o cabo na diagonal nessa direção -
06:04 a gente desenha ele
06:06 nessa direção aqui. Deixa eu tentar
06:09 mostrar o desenho para vocês.
06:11 Desenho nada, é uma figura 3D chiquérrima.
06:15 Então, tá aqui, e se a gente puser ela
06:19 nessa posição a gente vê, peraí...
06:23 que esse é o ponto (0,0) - vamos
06:27 tentar ignorar a coordenada z um
06:28 pouquinho... Esse é o ponto (1,0), esse
06:30 é o ponto (2,0), etc, esse é o ponto (1,1),
06:32 esse é o ponto (2,2), etc...
06:36 e essas diagonais daqui são os
06:41 cabos extras que eu vou desenhar...
06:44 e eu escolhi desenhar eles aqui porque em
06:46 todos os outros lugares
06:48 os quadrados vão virar retângulos em 3D
06:51 que são planos, e aqui eles virariam umas
06:54 coisas tortas... virariam tetraedros,
06:56 na verdade.
06:58 Então, se a gente começa a mudar o
07:01 ângulo dessa curva pra a gente ver ela
07:03 desse jeito a gente vê que nesse
07:07 pedaço dela em que eu desenhei o
07:11 cabo na diagonal num sentido "errado"
07:15 o que tá acontecendo aqui é que
07:20 tem um trecho...

07:24 metade desse quadrado daqui virou um
07:28 triângulo horizontal e metade virou um
07:30 outro triângulo que sobe bem rápido pra cá.
07:33 Tá, então isso faz bastante diferença, se
07:36 a gente olhar pra pirâmide de perfil
07:38 a gente vê que tem algo bem errado aí,
07:40 que ela não tem cara de pirâmide, tem um
07:42 degrau onde não deveria estar...
07:45 E... deixa eu voltar aqui pras figuras...

07:57 Então lembrem que a gente está
08:00 calculando as alturas só nos pontos com
08:03 coordenadas inteiras. Então a gente sabe
08:04 que todo mundo aqui tem altura 0, todo
08:07 mundo aqui tem altura 1... não, desculpa,
08:10 todo mundo aqui tem altura 1...
08:13 aqui tem altura 2... e a gente
08:17 poderia calcular as alturas nos outros
08:20 pontos
08:22 usando as fórmulas, porque quando
08:25 eu dei essa pirâmide daqui eu disse:
08:28 a fórmula que dá a altura dessa superfície
08:30 é essa aqui, é uma fórmula complicada com
08:33 mínimos e máximos... façam desenhos
08:35 de determinadas sub-funções,
08:38 tentem visualizar que que isso
08:42 quer dizer, e aí façam um diagrama de
08:44 numerozinhos e tentam desenhar a pirâmide.
08:48 Algumas pessoas devem ter conseguido
08:51 desenhar as funções mais básicas,
08:55 como essa daqui, que daria isso...
09:02 algumas pessoas devem ter conseguido
09:05 desenhar isso com facilidade, e elas
09:08 devem ter prática suficiente nessas
09:10 coisas pra saber que aqui a gente tá
09:12 subindo com...
09:16 bom, isso aqui tem coeficiente angular
09:18 constante, isso aqui também tem, aqui a gente
09:21 tá subindo a 45 graus, aqui a gente tá
09:24 descendo a 45 graus, etc... então algumas
09:28 pessoas sabem visualizar tudo isso
09:32 mais ou menos rápido,
09:33 e conseguem ver rapidamente que...
09:37 sem nem precisar fazer muita conta, no
09:39 olhômetro mesmo, que aqui a altura é 0.5,
09:43 aqui também é 0.5, aqui também é 0.5, etc...
09:46 então elas conseguem ver que todo mundo
09:48 aqui tem altura 1,
09:51 esse é o único ponto com altura 2,
09:54 todos esses pontos aqui têm altura 0,
09:59 e esses pontos aqui têm altura 0.5, tá...
10:05 no computador a gente pode pedir pra ele
10:08 pra calcular todos os pontos e
10:10 fazer uma figura bem mais precisa, mas
10:13 como a gente tá fazendo tudo à mão e
10:16 de cabeça a gente não pode fazer isso, a
10:18 gente tem que otimizar os nossos esforços
10:20 de alguma forma.

10:23 Então em princípio vocês tem que tentar
10:26 "adivinhar", entre aspas, qual é o
10:29 comportamento dessa figura, da
10:31 pirâmide, dentro desse quadrado
10:34 daqui, que é um dos quadrados complicados,
10:35 e dentro desse daqui, e aí tem vários
10:39 métodos possíveis... ou vocês calculam
10:41 a altura desses pontos do meio, pra aí
10:44 deduzir qual é o comportamento, ou vocês
10:46 de alguma outra forma deduzem que todo
10:49 mundo nessa reta daqui tem altura z=0.5,
10:54 ou vocês simplesmente pensam: que que
10:58 acontece se eu chutar? Então, tem dois
11:00 chutes naturais, um é imaginar que eu pus
11:04 um cabo na diagonal vindo daqui para cá,
11:06 ou eu pus um cabo na diagonal vindo daqui
11:08 para cá, e eu vou escolher qual os
11:10 dois é o meu preferido...
11:12 Então vamos ver o que acontece quando a
11:14 gente faz os dois chutes diferentes.
11:16 Então vamos ao Grande Truque de Chutar e
11:18 Testar, que é o que eu sempre recomendo em
11:21 Cálculo 2 e Cálculo 3...
11:22 façam os dois chutes, primeiro suponham
11:26 que o cabo é nessa direção, depois suponham
11:28 que ele é nessa direção, vejam com que
11:30 cara a figura fica... ou seja: testem...
11:32 e aí vejam se algum deles é mais razoável
11:35 que o outro...
11:37 e aí talvez vocês consigam fazer tudo
11:40 isso de cabeça, visualizando a coisa de
11:43 cabeça, talvez precisem de papel
11:47 quadriculado, uns palitos, sei lá,
11:49 umas coisas pra fazer um 3D improvisado
11:52 na mesa de vocês...

11:58 sei lá, tem todos esses métodos, mas
12:04 é isso, né, a gente tá tentando, como
12:06 sempre, descobrir superfícies a partir de
12:09 pouca informação, e aí tem vários chutes
12:12 razoáveis e a gente quer testar esses
12:14 chutes e ver qual dos dois é mais razoável...
12:17 se vocês fizerem o teste com o
12:20 cabo em diagonal aqui e outro
12:22 cabo em diagonal aqui vocês vão ter uma
12:26 figura bem esquisita - vocês vão ter
12:29 uma figura em que aqui a gente anda na
12:30 horizontal, aqui a gente sobe bem rápido,
12:32 aqui a gente anda na horizontal de novo,
12:33 aqui a gente sobe bem rápido, e ao invés
12:36 dela ser uma pirâmide
12:40 ela é feita de um monte de outras faces
12:42 mais complicadas... sei lá, tentem
12:44 imaginar isso, tá, eu não fiz a figura no
12:47 computador, é algo parecido com essa figura
12:51 que eu mostrei aqui...
12:53 cadê? Deixa eu ver...
13:00 parecido com essa,
13:05 só que a gente vai ter vários lugares
13:07 com essas coisas esquisitas em que uma
13:10 parte do quadrado tá horizontal e a
13:13 outra parte sobe bem rápido.
13:15 Então é isso. Tentem imaginar... e
13:19 imaginação é que nem músculo, à medida que
13:22 a gente vai exercitando ela fica mais
13:25 poderosa...
13:28 e assim que vocês tiverem mais prática
13:30 com esse tipo de figura vai ficar muito
13:32 mais fácil entender umas coisas de
13:34 derivadas parciais,
13:35 visualizar umas fórmulas do Bortolossi,
13:38 umas fórmulas do Silvanus Thompson, etc...
13:40 entre treinem, façam figuras,
13:43 mandem, etc. É isso por enquanto.

13:45