Eev hacks for Agda

I am trying to learn Agda. My brain seems to be wired in an atypical way, so I am trying to create notes, examples, and tests in a format that works well for me. I'm doing that for Org Mode too: see the video "Org for non-users".

My eev-based recipe for installing Agda on Debian is here.
It is based (IIRC!) on these instructions from PLFA.
To understand how I run that, see these slides.

I gave up trying to follow PLFA because I was getting stuck all the time on ideas that it pretends that are obvious... for example, its first chapters use only inductive types, but 1) I'm not very familiar with them, 2) my motivation for learning Agda was to formalize things like this, that use non-inductive types. But in one of these times in which I was stuck I tried to reread Martin-Löf's "Intuitionistic Type Theory" - for the n-th time in 20 years, for n big - and finally its canonical forms made sense to me...

I am now following Peter Selinger's lectures, and going back to PLFA occasionally.

Links to types and normal forms

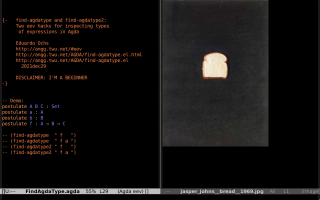
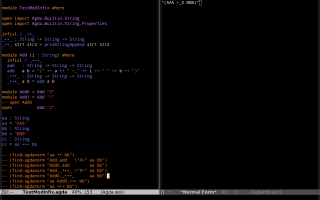
The video in the first thumbnail below - click to play it; its title is "find-agdatype and find-agdatype2 - two eev hacks for inspecting types of expressions in Agda" - explains the first non-trivial eev hack that I wrote for Agda. The second thumbnail below is a screenshot - click to enlarge it - that shows a similar hack, called "find-agdanorm", that I wrote some time after recording the video.

In short: we can put sexp hyperlinks like these in comments in an Agda file:

-- (find-agdatype "expr1")
-- (find-agdanorm "expr2")

Following the link (find-agdatype "expr1") shows the type of expr1 in the window at the right, and following the link (find-agdanorm "expr2") shows the result of normalizing expr2. The elisp code for find-agdatype and find-agdanorm is in find-agdatype.el. Here are some Agda files in which I used find-agdatype and find-agdanorm: Postulate1.agda, TestStrings.agda, TestPublic.agda.

Natural Deduction

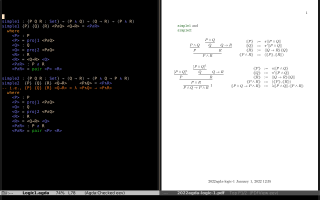
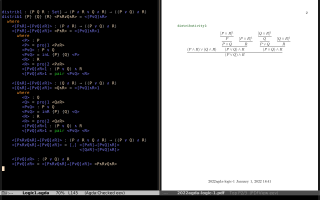
One exercise that I did was to translate some proofs in Natural Deduction to Agda - see the screenshots below. My code in Agda is in Logic1.agda and Logic2.lagda.tex, and the PDF that I used in the screenshots below is here.

Actually I first attempted to translate these proofs from PH2 to Agda, but I found that they were far above my level - and still are! - so I tried something more basic.

Some time after writing the proofs above I found a way to use Dednat6 in .lagda.tex files. The code still needs to be cleaned up, but here's an example of output... that, by the way, also shows how I am still struggling to write proofs of chains of equalities in a human-readable way. =/

Categories

I am trying to formalize this skeleton of a proof of the Yoneda Lemma in Agda. My current attempt is here; it is very incomplete, it needs diagrams, most of its symbols need to be renamed to match the diagrams, I haven't yet translated the proofs of functoriality from an older version to that one, etc, etc, etc... but I only learned how to write the composition in the category catB as B.o in 2022feb01! Work in progress!!!